За­да­ние 11 № 41569.

Вариант № 6999162

1. За­да­ние 1 № 505179. В лет­нем ла­ге­ре на каж­до­го участ­ни­ка по­ла­га­ет­ся 30 г са­ха­ра в день. В ла­ге­ре 103 че­ло­ве­ка. Сколь­ко ки­ло­грам­мо­вых упа­ко­вок са­ха­ра по­на­до­бит­ся на весь ла­герь на 6 дней?

Ре­ше­ние.

На 103 че­ло­века на 1 день по­ла­га­ет­ся 103 · 30 = 3090 г са­ха­ра, на 6 дней — 3090 · 6 = 18 540 г. Раз­де­лим 18 540 г на 1000 г в одной упа­ков­ке:

18 540: 1000 = 18,54.

Тем самым, на весь ла­герь на 6 дней 18 упа­ко­вок не хва­тит, сле­до­ва­тель­но, по­на­до­бит­ся 19 ки­ло­грам­мо­вых упа­ковок са­ха­ра.

Ответ: 19.

Ответ: 19

За­да­ние 2 № 28743.

На диа­грам­ме по­ка­за­но ко­ли­че­ство по­се­ти­те­лей сайта РИА Но­во­сти во все дни с 10 по 29 но­яб­ря 2009 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся дни ме­ся­ца, по вер­ти­ка­ли — ко­ли­че­ство по­се­ти­те­лей сайта за дан­ный день. Опре­де­ли­те по диа­грам­ме, сколь­ко было дней за дан­ный пе­ри­од, когда на сайте РИА Но­во­сти было менее по­лу­мил­ли­о­на по­се­ти­те­лей.

Ре­ше­ние.

Из диа­грам­мы видно, что было 3 дня, когда на сайте было менее по­лу­мил­ли­о­на по­се­ти­те­лей (см. ри­су­нок).

Ответ: 3.

Ответ: 3

За­да­ние 3 № 5453.

Семья из трех че­ло­век едет из Моск­вы в Че­бок­са­ры. Можно ехать по­ез­дом, а можно — на своей ма­ши­не. Билет на поезд на од­но­го че­ло­ве­ка стоит 930 руб­лей. Ав­то­мо­биль рас­хо­ду­ет 11 лит­ров бен­зи­на на 100 ки­ло­мет­ров пути, рас­сто­я­ние по шоссе равно 700 км, а цена бен­зи­на равна 18,5 руб­лей за литр. Сколь­ко руб­лей при­дет­ся за­пла­тить за наи­бо­лее де­ше­вую по­езд­ку на троих?

Ре­ше­ние.

Сто­и­мость по­езд­ки на по­ез­де для троих че­ло­век будет со­став­лять 930 3 = 2790 руб. Рас­ход бен­зи­на на 700 км пути со­ста­вит 7 раз по 11 лит­ров т. е. 77 лит­ров. Его сто­и­мость 77 18,5 = 1424,5 руб.

Сто­и­мость самой де­ше­вой по­езд­ки со­став­ля­ет 1424,5 рубля.

Ответ: 1424,5.

Ответ: 1424,5

1424,5

4. За­да­ние 4 № 27716. Диа­го­на­ли ромба равны 12 и 16. Най­ди­те длину век­то­ра .

Ре­ше­ние.

Раз­ность век­то­ров равна век­то­ру . Диа­го­на­ли ромба пер­пен­ди­ку­ляр­ны и точ­кой пе­ре­се­че­ния де­лят­ся по­по­лам. Пусть — точка пе­ре­се­че­ния диа­го­на­лей. Век­тор яв­ля­ет­ся ги­по­те­ну­зой в пря­мо­уголь­ном тре­уголь­ни­ке По­это­му .

Ответ: 10.

Ответ: 10

5. За­да­ние 5 № 320194. В груп­пе ту­ри­стов 30 че­ло­век. Их вер­толётом в не­сколь­ко приёмов за­бра­сы­ва­ют в труд­но­до­ступ­ный район по 6 че­ло­век за рейс. По­ря­док, в ко­то­ром вер­толёт пе­ре­во­зит ту­ри­стов, слу­ча­ен. Най­ди­те ве­ро­ят­ность того, что ту­рист П. по­ле­тит пер­вым рей­сом вер­толёта.

Ре­ше­ние.

На пер­вом рейсе 6 мест, всего мест 30. Тогда ве­ро­ят­ность того, что ту­рист П. по­ле­тит пер­вым рей­сом вер­толёта, равна:

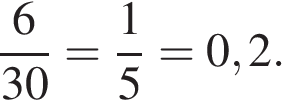
Ответ: 0,2.

Ответ: 0,2

0,2

6. За­да­ние 6 № 26656. Най­ди­те ко­рень урав­не­ния .

Ре­ше­ние.

Воз­ве­дем в квад­рат:

Ответ: 3.

Ответ: 3

7. За­да­ние 7 № 53665. Най­ди­те ра­ди­ус окруж­но­сти, впи­сан­ной в пра­виль­ный ше­сти­уголь­ник со сто­ро­ной

Ре­ше­ние.

Про­ве­дем по­стро­е­ния как по­ка­за­но на ри­сун­ке. Угол между сто­ро­на­ми пра­виль­но­го ше­сти­уголь­ни­ка равен 120°. Тре­уголь­ник 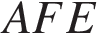— рав­но­бед­рен­ный, — вы­со­та, сле­до­ва­тель­но, — ме­ди­а­на и бис­сек­три­са, от­ку­да Из пря­мо­уголь­но­го тре­уголь­ни­ка

Ответ: 96.

Ответ: 96

8. За­да­ние 8 № 8297. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−6; 5). Най­ди­те про­ме­жут­ки убы­ва­ния функ­ции f(x). В от­ве­те ука­жи­те сумму целых точек, вхо­дя­щих в эти про­ме­жут­ки.

Ре­ше­ние.

Про­ме­жут­ки убы­ва­ния функ­ции f(x) со­от­вет­ству­ют про­ме­жут­кам, на ко­то­рых про­из­вод­ная функ­ции от­ри­ца­тель­на, то есть ин­тер­ва­лам (−6; −4,5) и (−0,5; 4,8). Дан­ные ин­тер­ва­лы со­дер­жит сле­ду­ю­щие целые точки: −5, 0, 1, 2, 3, 4 сумма ко­то­рых равна 5.

Ответ: 5.

Ответ: 5

9. За­да­ние 9 № 25889. Най­ди­те пло­щадь по­верх­но­сти мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке (все дву­гран­ные углы пря­мые).

Ре­ше­ние.

Пло­щадь по­верх­но­сти за­дан­но­го мно­го­гран­ни­ка равна сумме пло­ща­дей па­рал­ле­ле­пи­пе­дов со сто­ро­на­ми 3, 3, 4 и 5, 6, 2 умень­шен­ной на удво­ен­ную пло­щадь пря­мо­уголь­ни­ка со сто­ро­на­ми 4, 3:

.

Ответ: 146.

Ответ: 146

10. За­да­ние 10 № 26854. Най­ди­те зна­че­ние вы­ра­же­ния .

Ре­ше­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

.

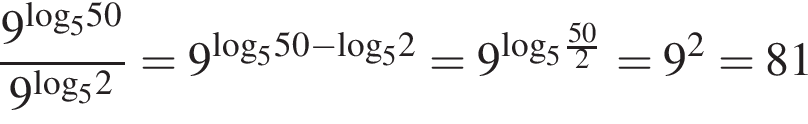Ответ: 81.

Ответ: 81

За­да­ние 11 № 41569.

Мо­то­цик­лист, дви­жу­щий­ся по го­ро­ду со ско­ро­стью км/ч, вы­ез­жа­ет из него и сразу после вы­ез­да на­чи­на­ет раз­го­нять­ся с по­сто­ян­ным уско­ре­ни­ем км/ч . Рас­сто­я­ние от мо­то­цик­ли­ста до го­ро­да, из­ме­ря­е­мое в ки­ло­мет­рах, опре­де­ля­ет­ся вы­ра­же­ни­ем . Опре­де­ли­те наи­боль­шее время, в те­че­ние ко­то­ро­го мо­то­цик­лист будет на­хо­дить­ся в зоне функ­ци­о­ни­ро­ва­ния со­то­вой связи, если опе­ра­тор га­ран­ти­ру­ет по­кры­тие на рас­сто­я­нии не далее чем в 45 км от го­ро­да. Ответ вы­ра­зи­те в ми­ну­тах.

Ре­ше­ние.

Мо­то­цик­лист будет на­хо­дить­ся в зоне функ­ци­о­ни­ро­ва­ния со­то­вой связи, если 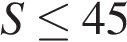км. За­да­ча сво­дит­ся к на­хож­де­нию наи­боль­ше­го ре­ше­ния не­ра­вен­ства 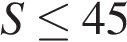км при за­дан­ных зна­че­ни­ях па­ра­мет­ров и :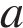

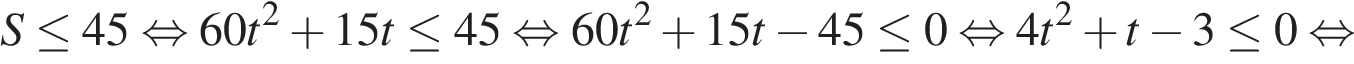
Учи­ты­вая то, что время — не­от­ри­ца­тель­ная ве­ли­чи­на, по­лу­ча­ем ч, то есть мин.

Ответ: 45.

Ответ: 45

12. За­да­ние 12 № 73625. 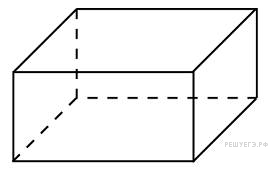Три ребра пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да, вы­хо­дя­щие из одной вер­ши­ны, равны 1, 4 и 2. Най­ди­те ребро рав­но­ве­ли­ко­го ему куба.

Ре­ше­ние.

Объем куба равен объ­е­му па­рал­ле­ле­пи­пе­да

Зна­чит, ребро куба

Ответ: 2.

Ответ: 2

13. За­да­ние 13 № 114785. Часы со стрел­ка­ми по­ка­зы­ва­ют 3 часа ровно. Через сколь­ко минут ми­нут­ная стрел­ка в де­вя­тый раз по­рав­ня­ет­ся с ча­со­вой?

Ре­ше­ние.

Ско­рость дви­же­ния ми­нут­ной стрел­ки 12 де­ле­ний/час (под одним де­ле­ни­ем здесь под­ра­зу­ме­ва­ет­ся рас­сто­я­ние между со­сед­ни­ми циф­ра­ми на ци­фер­бла­те часов), а ча­со­вой – 1 де­ле­ние/час. До де­вя­той встре­чи ми­нут­ной и ча­со­вой стре­лок ми­нут­ная долж­на сна­ча­ла 8 раз «обо­гнать» ча­со­вую, то есть прой­ти 8 кру­гов по 12 де­ле­ний. Пусть после этого до по­след­ней встре­чи ча­со­вая стрел­ка прой­дет де­ле­ний. Тогда общий путь ми­нут­ной стрел­ки скла­ды­ва­ет­ся из най­ден­ных 96 де­ле­ний, ещё 3 из­на­чаль­но раз­де­ля­ю­щих их де­ле­ний (по­сколь­ку часы по­ка­зы­ва­ют 3 часа) и по­след­них L де­ле­ний. При­рав­ня­ем время дви­же­ния для ча­со­вой и ми­нут­ной стре­лок:

.

Ча­со­вая стрел­ка прой­дет 9 де­ле­ний, что со­от­вет­ству­ет 9 часам или 540 ми­ну­там.

Ответ: 540.

Ответ: 540

Дата добавления: 2015-10-26