За­да­ние 6 № 13685.

Ре­ше­ние.

Для по­крас­ки 50 кв. м. по­тол­ка по­тре­бу­ет­ся 50 · 240 = 12 000 г = 12 кг крас­ки. Раз­де­лим 12 на 2,5, по­лу­чим 4,8. Сле­до­ва­тель­но, по­тре­бу­ет­ся 5 банок крас­ки.

Ответ: 5.

Ответ: 5

2. За­да­ние 2 № 26874. На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­на цена зо­ло­та на мо­мент за­кры­тия бир­же­вых тор­гов во все ра­бо­чие дни с 5 по 28 марта 1996 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся числа ме­ся­ца, по вер­ти­ка­ли — цена унции зо­ло­та в дол­ла­рах США. Для на­гляд­но­сти жир­ные точки на ри­сун­ке со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку, ка­ко­го числа цена зо­ло­та на мо­мент за­кры­тия тор­гов была наи­мень­шей за дан­ный пе­ри­од.

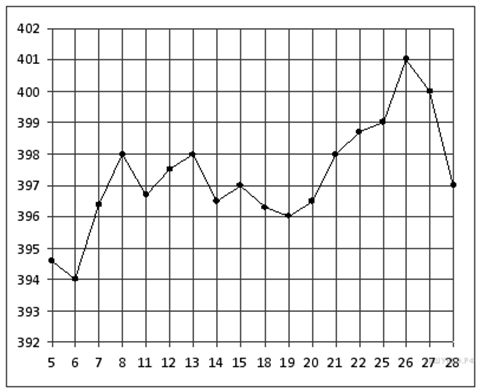
Ре­ше­ние.

Из гра­фи­ка видно, что наи­мень­шей цена была 6 марта (см. ри­су­нок).

Ответ: 6.

Ответ: 6

3. За­да­ние 3 № 319557. Рей­тин­го­вое агент­ство опре­де­ля­ет рей­тинг со­от­но­ше­ния «цена-ка­че­ство» элек­три­че­ских фенов для волос. Рей­тинг вы­чис­ля­ет­ся на ос­но­ве сред­ней цены 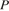и оце­нок функ­ци­о­наль­но­сти 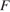, ка­че­ства и ди­зай­на . Каж­дый от­дель­ный по­ка­за­тель оце­ни­ва­ет­ся экс­пер­та­ми по пя­ти­балль­ной шкале це­лы­ми чис­ла­ми от 0 до 4. Ито­го­вый рей­тинг вы­чис­ля­ет­ся по фор­му­ле

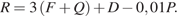
В таб­ли­це даны оцен­ки каж­до­го по­ка­за­те­ля для не­сколь­ких мо­де­лей фенов. Опре­де­ли­те, какая мо­дель имеет наи­мень­ший рей­тинг. В ответ за­пи­ши­те зна­че­ние этого рей­тин­га.

Мо­дель фена	Сред­няя цена	Функ­ци­о­наль­ность	Ка­че­ство	Ди­зайн
А
Б
В
Г

Ре­ше­ние.

Рас­смот­рим все ва­ри­ан­ты.

Мо­дель А:

Мо­дель Б: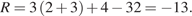

Мо­дель В: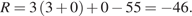

Мо­дель Г: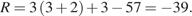

Таким об­ра­зом, наи­мень­ший рей­тинг имеет мо­дель В. Он равен −46.

Ответ: −46.

Ответ: -46

-46

4. За­да­ние 4 № 27811. 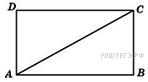Най­ди­те диа­го­наль пря­мо­уголь­ни­ка, две сто­ро­ны ко­то­ро­го равны и .

Ре­ше­ние.

по тео­ре­ме Пи­фа­го­ра диа­го­наль равна .

Ответ: 10.

Ответ: 10

За­да­ние 5 № 321035.

Перед на­ча­лом фут­боль­но­го матча судья бро­са­ет мо­нет­ку, чтобы опре­де­лить, какая из ко­манд начнёт игру с мячом. Ко­ман­да «Сап­фир» иг­ра­ет три матча с раз­ны­ми ко­ман­да­ми. Най­ди­те ве­ро­ят­ность того, что в этих играх «Сап­фир» вы­иг­ра­ет жре­бий ровно два раза.

Ре­ше­ние.

Обо­зна­чим «1» ту сто­ро­ну мо­не­ты, ко­то­рая от­ве­ча­ет за вы­иг­рыш жре­бия «Сап­фир», дру­гую сто­ро­ну мо­не­ты обо­зна­чим «0». Тогда бла­го­при­ят­ных ком­би­на­ций три: 110, 101, 011, а всего ком­би­на­ций 2³ = 8: 000, 001, 010, 011, 100, 101, 110, 111. Тем самым, ис­ко­мая ве­ро­ят­ность равна:

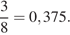
Ответ: 0,375.

Ответ: 0,375

0,375

За­да­ние 6 № 13685.

Най­ди­те ко­рень урав­не­ния: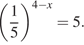

Ре­ше­ние.

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

.

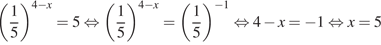Ответ: 5.

Ответ: 5

7. За­да­ние 7 № 27881. Най­ди­те угол 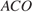, если его сто­ро­на 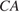ка­са­ет­ся окруж­но­сти, – центр окруж­но­сти, а мень­шая дуга окруж­но­сти 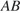, за­клю­чен­ная внут­ри этого угла, равна . Ответ дайте в гра­ду­сах.

Ре­ше­ние.

ка­са­тель­ная к окруж­но­сти пер­пен­ди­ку­ляр­на ра­ди­у­су, цен­траль­ный угол равен дуге, на ко­то­рую он опи­ра­ет­ся, зна­чит, тре­уголь­ник 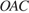– пря­мо­уголь­ный и

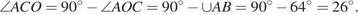
Ответ: 26.

Ответ: 26

Дата добавления: 2015-10-26