|
Читайте также: |
Прямая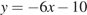 
является касательной к графику функции 
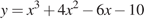. Найдите абсциссу точки касания.
Решение.
Условие касания графика функции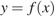 
и прямой 
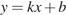задаётся системой требований:
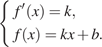
В нашем случае имеем:
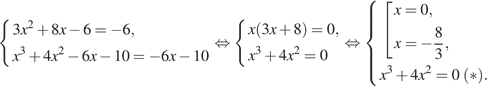
Проверка показывает, что первый корень удовлетворяет, а второй не удовлетворяет уравнению (*). Поэтому искомая абсцисса точки касания 0.
Ответ: 0.
Ответ: 0
9. Задание 9 № 509015.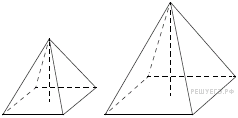 
Даны две правильные четырёхугольные пирамиды. Объём первой пирамиды равен 16. У второй пирамиды высота в 2 раза больше, а сторона основания в 1,5 раза больше, чем у первой. Найдите объём второй пирамиды.
Решение.
Объём пирамиды вычисляется по формуле 
Следовательно, отношение объёмов пирамид:
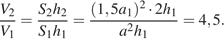
Значит, объём второй пирамиды: 16 · 4,5 = 72.
Ответ: 72.
Ответ: 72
Источник: СтатГрад: Диагностическая работа по математике 13.02.2015 вариант МА00409.
10. Задание 10 № 77398. Найдите значение выражения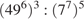 
.
Решение.
Выполним преобразования:
.
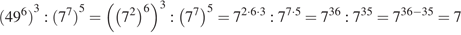Ответ: 7.
Ответ: 7
11. Задание 11 № 319860. Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности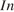 
, оперативности 
, объективности публикаций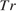 
, а также качества сайта 
. Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от -2 до 2.
Аналитики, составляющие формулу рейтинга, считают, что объективность ценится втрое, а информативность публикаций — впятеро дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид
Если по всем четырем показателям какое-то издание получило одну и ту же оценку, то рейтинг должен совпадать с этой оценкой. Найдите число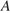 
, при котором это условие будет выполняться.
Решение.
Обозначим совпадающую оценку по разным показателям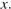 
Поскольку все показатели равны друг другу, все они равны 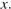Подставим значения в формулу, учитывая, что рейтинг равен 
:
Ответ:10.
Ответ: 10
12. Задание 12 № 27159. 
Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на 
.
Решение.
Площадь поверхности складывается из площади основания 
и площади боковой поверхности:
.
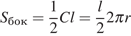Радиус основания найдем по теореме Пифагора для треугольника, образованного высотой, образующей и радиусом: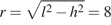 
. Тогда площадь поверхности
Ответ: 144.
Ответ: 144
13. Задание 13 № 39213. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 180 км. На следующий день он отправился обратно в А со скоростью на 8 км/ч больше прежней. По дороге он сделал остановку на 8 часов. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
Решение.
Пусть 
км/ч — скорость велосипедиста на пути из B в A, тогда скорость велосипедиста на пути из A в B равна 
км/ч. Сделав на обратном пути остановку на 8 часов, велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B, отсюда имеем:
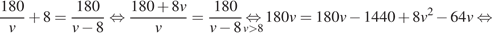
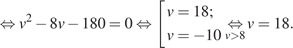
Таким образом, скорость велосипедиста была равна 18 км/ч.
Ответ: 18.
Ответ: 18
14. Задание 14 № 129871. Найдите точку максимума функции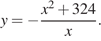 
Решение.
Найдем производную заданной функции:
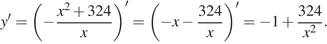
Найдем нули производной:
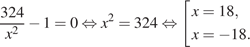
Определим знаки производной функции и изобразим на рисунке поведение функции:
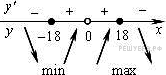
Искомая точка максимума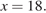 
Ответ: 18.
Ответ: 18
15. Задание 15 № 505470. а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку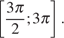 
Решение.
а) Преобразуем исходное уравнение:
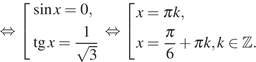
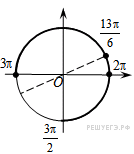б) С помощью числовой окружности отберём корни, принадлежащие отрезку 
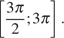Получим числа: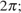 
Ответ: а)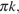 
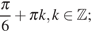б)
Источник: ЕГЭ по математике 05.06.2014. Основная волна. Восток. Вариант 1.
16. Задание 16 № 503361. В правильную четырёхугольную пирамиду, боковое ребро которой равно 17, а высота равна 7, вписана сфера. (Сфера касается всех граней пирамиды.) Найдите площадь этой сферы.
Решение.
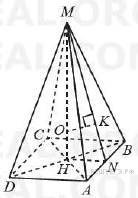Пусть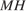 
— высота правильной четырёхугольной пирамиды 
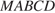с вершиной 
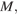тогда треугольник 
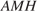— прямоугольный, 
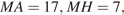откуда
Треугольник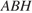 
— прямоугольный равнобедренный, следовательно, 
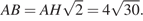В треугольнике 
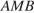высота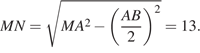 
В равнобедренном прямоугольном треугольнике 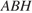высота 
Центр 
сферы, вписанной в правильную четырёхугольную пирамиду, лежит на её высоте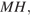 
точка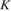 
касания сферы и боковой грани 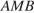лежит на отрезке 
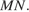Треугольники 
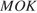и 
подобны, поэтому
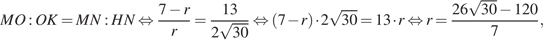
где 
— радиус сферы.
Площадь сферы 
Ответ: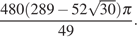 
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 702.
17. Задание 17 № 508512. Решите неравенство: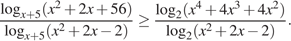 
Решение.
Заметим, что пр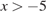и 
и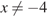 
исходное неравенство равносильно неравенству:
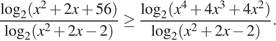
Положив в последнем неравенстве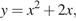 
получаем:
Далее имеем:
Учитывая то, что 
получаем решения второго неравенства: 
Ответ:
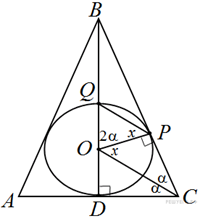
18. Задание 18 № 504832. Окружность с центром O, вписанная в треугольник ABC, касается стороны BC в точке P и пересекает отрезок BO в точке Q. При этом отрезки OC и QP параллельны.
а) Докажите, что треугольник ABC ― равнобедренный треугольник.
б) Найдите площадь треугольника BQP, если точка O делит высоту BD треугольника в отношении BO: OD = 3:1 и AC = 2 a.
Решение.
Пусть луч 
пересекает сторону 
в точке 
Введем следующие обозначения: 
, 
. Прямые 
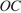и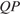 
параллельны, а углы 
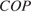и 
― накрест лежащие при пересечении прямых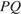 
и 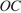секущей 
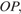следовательно 
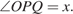Далее, из прямоугольного треугольника 
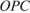находим 
, а из равнобедренного треугольника находим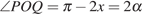 
. Таким образом, треугольник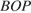и 
и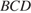 
подобны, и, значит, биссектриса 
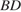треугольника 
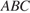является его высотой, откуда следует, что треугольник 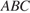― равнобедренный треугольник, что и требовалось доказать.
б) Отрезок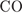 
― биссектриса треугольника 
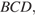следовательно:
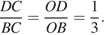
Откуда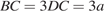 
.
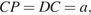значит 
и, следовательно: 
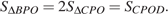Откуда 
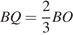, следовательно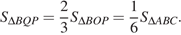 
По формуле Герона находим:
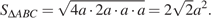
Значит,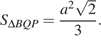 
Ответ: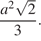 
Источник: Пробный экзамен по математике Санкт-Петербург 2014. Вариант 1.
19. Задание 19 № 508257. В 1-е классы поступает 43 человека: 23 мальчика и 20 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом ― 21. После распределения посчитали процент мальчиков в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей?
Решение.
Решение 1. Вместо суммарного процента будем считать суммарную долю мальчиков ― очевидно, эти числа отличаются в 100 раз и достигают своего максимума одновременно. Каждый мальчик в классе из 22 человек составляет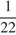 
от общего числа учащихся в этом классе, а в классе из 21 человек ― 
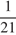от общего числа учащихся. Значит, если поменять местами девочку из меньшего класса и мальчика из большего, суммарный процент мальчиков вырастет. Таким образом, максимум достигается, когда все подобные перестановки сделаны, то есть, когда меньший класс полностью состоит из мальчиков, а в большем классе ― 20 девочек и 2 мальчика.
Решение 2. Пусть в меньший класс распределено х мальчиков (где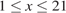 
), тогда в больший класс попало (
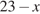) мальчиков. Значит, суммарная доля мальчиков в двух классах равна 
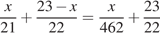и представляет собой линейную функцию с положительным угловым коэффициентом. Значит, эта функция достигает своего наибольшего значения на правом конце промежутка [1; 21], то есть при 
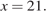Таким образом, меньший класс полностью должен состоять из мальчиков, а в большем классе должно быть 20 девочки и 2 мальчика.
Ответ: В одном классе ― 21 мальчик, в другом ― 20 девочек и 2 мальчика.
Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 2.
20. Задание 20 № 500965. Найдите все значения параметра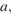 
при каждом из которых на интервале 
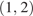существует хотя бы одно число 
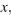неудовлетворяющее неравенству 
Решение.
Преобразуем неравенство:
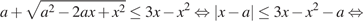
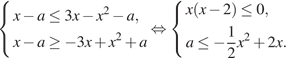
Неравенство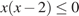 
определяет на плоскости 
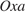полосу, заключенную между прямыми 
и 
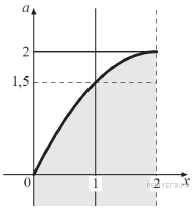
Неравенство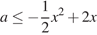 
задаёт часть плоскости, ограниченную сверху параболой.
На рисунке видно, что на интервале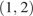 
есть 
, не удовлетворяющие неравенству, только если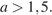 
Ответ: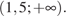 
Источник: МИОО: Диагностическая работа по математике 18.12.2012 вариант 5.
21. Задание 21 № 484664. Найдите все простые числа p, для каждого из которых существует такое целое число k, что число p является общим делителем чисел 
и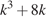 
.
П/п
Задания
Ответ
-46
0,375
Дата добавления: 2015-10-26; просмотров: 524 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задание 6 № 13685. | | | Как опубликовать статью |