|
Читайте также: |
Найдите наибольшее значение функции 
на отрезке 
.
Решение.
Найдем производную заданной функции:
Найденная производная неотрицательна на заданном отрезке, заданная функция возрастает на нем, поэтому наибольшим значением функции на отрезке является
Ответ: 23.
Ответ: 23
15. Задание 15 № 505240. а) Решите уравнение 
б) Найдите все корни этого уравнения, принадлежащие промежутку 
Решение.
а) Левая часть уравнения определена, есл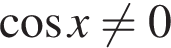и 
и 
При этом 
Поэтому уравнение можно переписать в виде 
Решив последнее уравнение как квадратное относительно 
получим 
или 
Значит, либо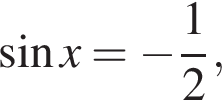 
откуда 
либо 
что невозможно в силу условия 
б) Отберем с помощью единичной окружности отберём корни, принадлежащие промежутку 
(см. рис.):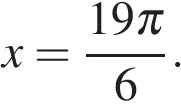 
Ответ: а) 
б) 
16. Задание 16 № 500213. На ребре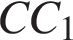 
куба 
отмечена точка 
так, что 
Найдите угол между прямыми 
и 
Решение.
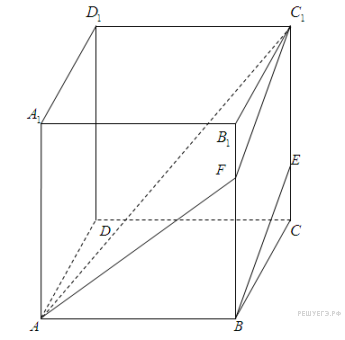Примем ребро куба за 
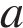. Тогда 
Поскольку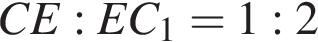 
, получаем: 
и 
Проведем через точку 
прямую, параллельную . Она пересекает ребро 
в точке 
, причем треугольники 
и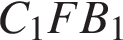 
равны. Искомый угол равен углу 
(или смежному с ним).
В прямоугольном треугольнике 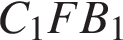с прямым углом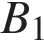 
В прямоугольном треугольнике 
с прямым углом 
В треугольнике
откуда
Тогда 
Ответ может быть представлен и в другом виде: 
или 
Ответ: 
17. Задание 17 № 507817. Решите неравенство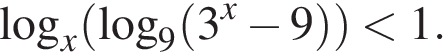 
Решение.
Поскольку 
сразу имеем x > 2, и функция 
возрастает. Поэтому 
Это значит, что 
Для первого неравенства имеем 
Второе неравенство выполнено всегда, так как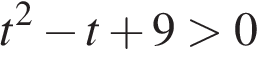 
при всех t из-за отрицательности дискриминанта (замена 
). Таким образом, 
Ответ: 
Источник: МИОО: Тренировочная работа по математике, ноябрь 2009 года вариант 1. (Часть С)
18. Задание 18 № 500009. Дан треугольник АВС, площадь которого равна 55. Точка Е на прямой АС выбрана так, что треугольник АВЕ ― равнобедренный с основанием АЕ и высотой BD. Найдите площадь треугольника АВE, если известно, что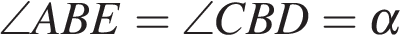 
и 
.
Решение.
Введем следующие обозначения: 
, 
, 
.
1 случай (точка E лежит между точками A и С, см. рис. 1).
Треугольник АВЕ равнобедренный, поэтому 
, а значит,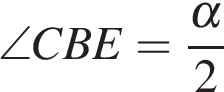 
.
Углы ABE и CBD треугольников ABE и CBD равны, значит,
,
откуда 
.
Поскольку 
, получаем
,
откуда
,
значит,
.
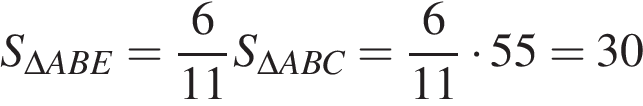2 случай (точка A лежит между точками E и С, см. рис. 2).
Аналогично случаю 1 находим
.
Ответ: 30 или 66.
19. Задание 19 № 506951. Банк под определенный процент принял некоторую сумму. Через год четверть накопленной суммы была снята со счета. Банк увеличил процент годовых на 40%. К концу следующего года накопленная сумма в 1,44 раза превысила первоначальный вклад. Каков процент новых годовых?
Решение.
Пусть банк первоначально принял вклад в размере 
у.е. под 
годовых. Тогда к началу второго года сумма стала 
у.е.
После снятия четверти накопленной суммы на счету осталось 
у.е.
С момента увеличения банком процентной ставки на 40% к концу второго года хранения остатка вклада накопленная сумма стала
у.е.
По условию задачи эта сумма равна 
у.е.
Решим уравнение 
; 
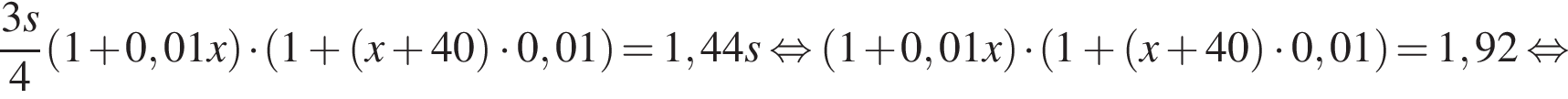
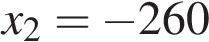
Этот корень не подходит по смыслу задачи: 
Новые годовые составляют 20 + 40 = 60 %.
Ответ: 60.
Источник: А. Ларин: Тренировочный вариант № 84.
20. Задание 20 № 484634. При каких значениях параметра 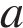хотя бы при одном значении параметра с система
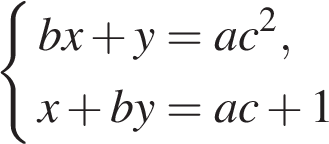
имеет решения для любых значений параметра 
?
Решение.
Ясно, что при 
система имеет единственное решение
которое выражается через 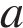и 
однозначно, то есть существует для любых 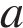и .
При 
, если умножить второе уравнение на b и из полученного уравнения вычесть первое уравнение системы, то будем иметь
.
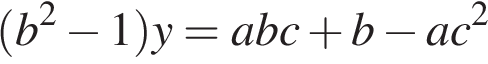Если же умножить на b первое уравнение и из полученного уравнения вычесть второе уравнение системы, то
.
Таким образом, исходная система равносильна системе
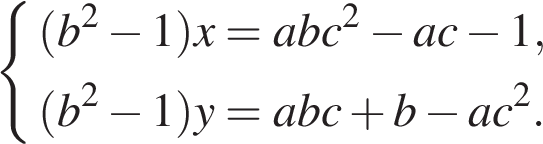
При любом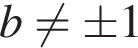 
система всегда имеет единственное решение.
Если же 
, то система будет иметь решения если существуют 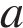и удовлетворяющие уравнению
.
Рассматривая его как квадратное относительно параметра с, приходим к выводу, что оно будет иметь хотя бы одно решение, если 
и 
, т. е. если 
.
При 
приходим к рассмотрению уравнения
.
В данном случае решая неравенство 
, где , находим, что 
.
Ответ: 
.
21. Задание 21 № 500005. На доске написано число 7. Раз в минуту Вася дописывает на доску одно число: либо вдвое большее какого-то из чисел на доске, либо равное сумме каких-то двух чисел, написанных на доске (таким образом, через одну минуту на доске появится второе число, через две ― третье и т.д.).
а) Может ли в какой-то момент на доске оказаться число 2012?
б) Может ли в какой-то момент сумма всех чисел на доске равняться 63?
в) Через какое наименьшее время на доске может появиться число 784?
Решение.
а) Заметим, что каждое число на доске будет делиться на 7. Действительно, исходное число делится на 7, в случае удвоения числа делящегося на 7, получится число, делящееся на 7. А при сложении чисел, делящихся на 7, также получится число, делящееся на 7. Таким образом, все числа на доске будут делиться на 7, а 2012 на 7 не делится, следовательно, оно не может появиться на доске.
б) Да, может. Пример: 7, 14 (удвоенное число 7), 14 (удвоенное число 7), 14 (удвоенное число 7), 14 (удвоенное число 7). Сумма полученных 5 чисел равна 63.
Замечание. В условии не сказано, что одно число нельзя удваивать несколько раз.
в) Как было замечено в пункте а), все числа на доске будут делиться на 7. Рассмотрим аналогичную задачу, разделив исходное число 7 и то число, которое нужно получить, то есть 784, на 7. От этого количество операций не изменится. Таким образом, достаточно за наименьшее количество операций получить число 112, начав с числа 1.
Заметим, что наибольшее число, которое может получиться на доске через 6 минут, равно 64 (если Вася каждый раз будет удваивать текущее наибольшее число). Следовательно, если в первые 6 минут Вася каждый раз удваивал наибольшее число на доске, то число 112 нельзя получить за 7 минут: если число 64 удвоить, то получится 128, а если прибавить к нему число, не превосходящее 32, то 112 не получится.
В том случае, если в течение первых 6 минут Вася использовал хотя бы одно сложение вместо удвоения, то при первом использовании сложения наибольшее число, записанное на доске увеличилось не более, чем в полтора раза: действительно, в этом случае самый большой результат получится тогда, когда мы к максимальному на данный момент числу прибавим второе по величине, то есть, его половину (напомним, что мы рассматриваем первый случай сложения, то есть до этого были только удвоения). Таким образом, даже если в течение первых 7 минут сделано 6 удвоений и одно сложение (в некотором порядке), то наибольшее число, которое может получиться, равно 96, что меньше 112.
Итак, за 7 минут число 112 получить невозможно.
Приведем пример, как его получить за 8 минут:
Ответ: а) нет; б) да; в) 8 минут.
№ п/п № задания Ответ
1 506607 -0,21
2 507005 0,002
3 506629 6300000
4 507929 24
5 26766 -4
6 506759 9
7 27466 31
8 506511 564
9 506804 3241
10 285923 0,225
11 506091 4
12 500886 34
13 27053 9
14 125135 113
15 250947 0,5
16 324454 2
17 506643 1342
18 506771 14
19 508010 74535|75135|45135
20 506606 117700
Дата добавления: 2015-10-26; просмотров: 201 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задание 11 № 41569. | | | Задание 6 № 13685. |