
Читайте также:
|
При решении задач физического и геометрического содержания необходимо учесть, что исследуемая функция в готовом виде не дается, а определяется из условия задачи.
Во всех случаях, когда функция, определенная из условия задачи, окажется функцией двух независимых переменных, необходимо, используя данные задачи, одну из этих переменных исключить.
Задача 1. Для доставки продукции завода Д в город А строится шоссе ДР, соединяющее завод с железной дорогой АВ, проходящей через город А. Стоимость перевозок по шоссе вдвое больше, чем по железной дороге. К какому пункту Р нужно подвести шоссе, чтобы общая стоимость перевозок продукции завода Д в город А по маршруту ДРА была наименьшей? Известно, что АВ = 500 км,  и ДВ = 100 км (рис. 5).
и ДВ = 100 км (рис. 5).
Решение. Пусть пункт Р находится от А на расстоянии  , причем
, причем 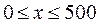 . Тогда
. Тогда  и из прямоугольного треугольника РДВ найдем гипотенузу РД:
и из прямоугольного треугольника РДВ найдем гипотенузу РД:  . Будем полагать, что стоимость провоза одной тонны груза на 1 км по железной дороге составляет одну условную единицу, а по шоссе (согласно условию задачи) – две условные единицы. Тогда, чтобы доставить одну тонну груза от завода Д до города А по маршруту ДРА надо затратить N условных единиц:
. Будем полагать, что стоимость провоза одной тонны груза на 1 км по железной дороге составляет одну условную единицу, а по шоссе (согласно условию задачи) – две условные единицы. Тогда, чтобы доставить одну тонну груза от завода Д до города А по маршруту ДРА надо затратить N условных единиц:  или
или 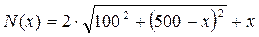 . Получена функция N(x), для которой надо найти наименьшее значение на отрезке
. Получена функция N(x), для которой надо найти наименьшее значение на отрезке  . Непрерывная и дифференцируемая на отрезке функция достигает наибольшего и наименьшего значения либо в конечных точках отрезка, либо в точках, в которых производная обращается в нуль. Найдем N(0) и N(500), а затем точки, для которых
. Непрерывная и дифференцируемая на отрезке функция достигает наибольшего и наименьшего значения либо в конечных точках отрезка, либо в точках, в которых производная обращается в нуль. Найдем N(0) и N(500), а затем точки, для которых  :
:
 ;
;
 ;
;
 и производная обращается в ноль, если
и производная обращается в ноль, если  . Решим уравнение и найдем значение переменной
. Решим уравнение и найдем значение переменной  . В полученной точке вычислим функцию
. В полученной точке вычислим функцию  . Сравним значения
. Сравним значения  ,
,  и
и  и сделаем вывод, что наименьшей стоимость перевозок будет, если пункт Р установить на расстоянии
и сделаем вывод, что наименьшей стоимость перевозок будет, если пункт Р установить на расстоянии 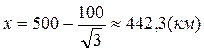 от города А.
от города А.

Рис. 5. Рисунок к задаче 1.
Задача 2. Требуется построить открытый цилиндрический резервуар вместимостью  . Материал имеет толщину
. Материал имеет толщину 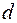 . Каковы должны быть размеры резервуара (радиус основания и высота), чтобы расход материала был наименьшим?
. Каковы должны быть размеры резервуара (радиус основания и высота), чтобы расход материала был наименьшим?
Решение.
Изобразим разрез резервуара (рис. 6). Радиус основания внутреннего цилиндра обозначим через  , высоту внутреннего цилиндра – через
, высоту внутреннего цилиндра – через  . Объём дна и стенки резервуара:
. Объём дна и стенки резервуара:


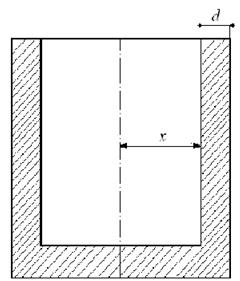
Рис. 6. Разрез резервуара
С другой стороны, по условию должно быть  , откуда
, откуда 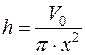 .
.
Подставив  в формулу объёма V, получим
в формулу объёма V, получим


Полученную функцию 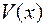 нужно исследовать на экстремум при
нужно исследовать на экстремум при 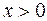 :
:

Единственное положительное значение  , при котором
, при котором  =0 – это
=0 – это  .
.
Оно и есть решение задачи, поскольку при переходе через эту точку производная меняет знак с минуса на плюс. При этом 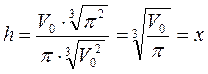 , т. е. высота внутреннего цилиндра равна радиусу внутреннего основания.
, т. е. высота внутреннего цилиндра равна радиусу внутреннего основания.
Задача 3. На какой высоте следует поместить источник света над освещенной поверхностью, чтобы освещение на расстоянии  от основания перпендикуляра, опущенного из источника света на освещенную поверхность, было наибольшим?
от основания перпендикуляра, опущенного из источника света на освещенную поверхность, было наибольшим?
Известно, что освещенность обратно пропорциональна квадрату расстояния от источника света и прямо пропорциональна синусу угла между лучом и освещенной поверхностью (рис. 7).

Рис. 7.
Решение.
Освещенность 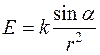 , где
, где  – коэффициент пропорциональности. Так как
– коэффициент пропорциональности. Так как
 , то
, то  ,
,
где 
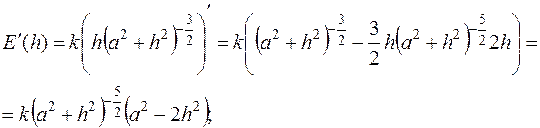
 при
при 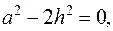 т.е.
т.е.  . При переходе через точку
. При переходе через точку  производная меняет знак с плюса на минус. Наибольшая освещенность
производная меняет знак с плюса на минус. Наибольшая освещенность 
ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
Задача 1. Построить графики функций с помощью производной первого порядка:
1. a)  б)
б) 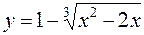
2. а)  б)
б) 
3. а) 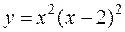 б)
б) 
4. а)  б)
б) 
5. а)  б)
б) 
6. а)  б)
б) 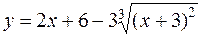
7. а)  б)
б) 
8. а)  б)
б) 
9. а)  б)
б) 
10. а) 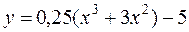 б)
б) 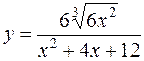
11. а)  б)
б) 
12. а)  б)
б) 
13. а)  б)
б) 
14. а)  б)
б) 
15. а)  б)
б) 
16. а)  б)
б) 
17. а)  б)
б) 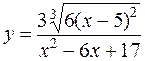
18. а)  б)
б) 
19. а)  б)
б) 
20. а)  б)
б) 
21. а)  б)
б) 
22. а) 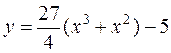 б)
б) 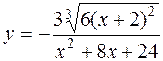
23. а) 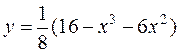 б)
б) 
24. а)  б)
б) 
25. а)  б)
б) 
26. а)  б)
б) 
27. а)  б)
б) 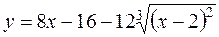
28. а) 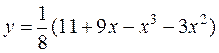 б)
б) 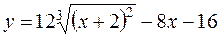
29. а)  б)
б) 
30. а)  б)
б) 
Задача 2. Найти наибольшее и наименьшее значения функции на отрезке:
1. 

2. 

3. 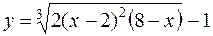

4. 

5. 

6. 

7. 

8. 

9. 

10. 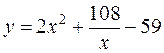

11. 

12. 

13. 

14. 
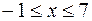
15. 

16. 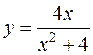

17. 

18. 

19. 

20. 

21. 

22. 

23. 

24. 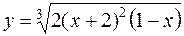
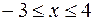
25. 

26. 

27. 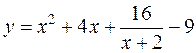

28. 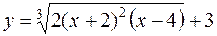

29. 

30. 

Задача 3. Найти асимптоты графика функции и построить график функции по точкам.
1.  2.
2.  3.
3. 
4.  5.
5.  6.
6. 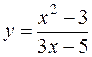
7.  8.
8.  9.
9. 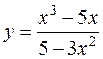
10.  11.
11. 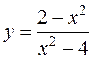 12.
12. 
13.  14.
14.  15.
15. 
16.  17.
17.  18.
18. 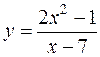
19.  20.
20.  21.
21. 
22.  23.
23. 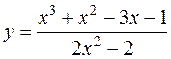 24.
24. 
25.  26.
26.  27.
27. 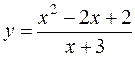
28.  29.
29. 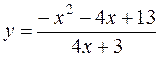 30.
30. 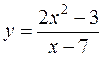
Задача 4. Провести полное исследование функций и построить их графики.
1. а)  б)
б)  в)
в) 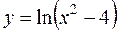
г)  д)
д) 
2. а)  б)
б)  в)
в) 
г)  д)
д) 
3. а)  б)
б)  в)
в) 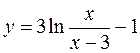
г)  д)
д) 
4. а)  б)
б)  в)
в) 
г)  д)
д) 
5. а)  б)
б) 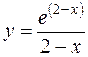 в)
в) 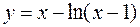
г) 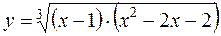 д)
д) 
6. а)  б)
б) 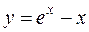 в)
в) 
г)  д)
д) 
7. а)  б)
б)  в)
в) 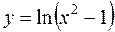
г)  д)
д) 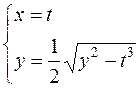
8. а)  б)
б)  в)
в) 
г)  д)
д) 
9. а)  б)
б)  в)
в) 
г)  д)
д) 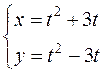
10. а) 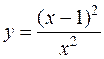 б)
б)  в)
в) 
г)  д)
д) 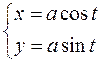
11. а)  б)
б)  в)
в) 
г)  д)
д) 
12. а)  б)
б)  в)
в) 
г)  д)
д) 
13. а)  б)
б) 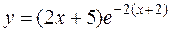 в)
в) 
г) 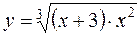 д)
д) 
14. а) 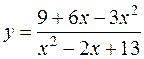 б)
б)  в)
в) 
г) 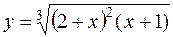 д)
д) 
15. а)  б)
б)  в)
в) 
г)  д)
д) 
16. а) 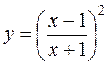 б)
б)  в)
в) 
г)  д)
д) 
17. а)  б)
б)  в)
в) 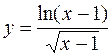
г)  д)
д) 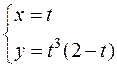
18. а)  б)
б)  в)
в) 
г)  д)
д) 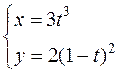
19. а)  б)
б)  в)
в) 
г)  д)
д) 
20. а)  б)
б)  в)
в) 
г)  д)
д) 
21. а)  б)
б)  в)
в) 
г) 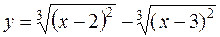 д)
д) 
22. а)  б)
б)  в)
в) 
г)  д)
д) 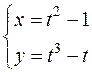
23. а) 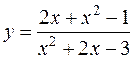 б)
б)  в)
в) 
г) 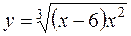 д)
д) 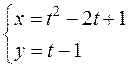
24. а)  б)
б)  в)
в) 
г) 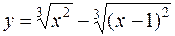 д)
д) 
25. а)  б)
б)  в)
в) 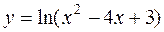
г)  д)
д) 
26. а)  б)
б) 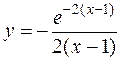 в)
в) 
г)  д)
д) 
27. а)  б)
б)  в)
в) 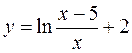
г)  д)
д) 
28. а)  б)
б)  в)
в) 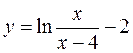
г) 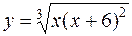 д)
д) 
29. а)  б)
б)  в)
в) 
г) 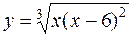 д)
д) 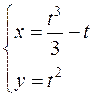
30. а)  б)
б) 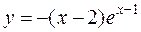 в)
в) 
г)  д)
д) 
Задача 5. Построить по точкам графики функций, заданных в полярных координатах.
1. а)  б)
б) 

2. а)  б)
б) 
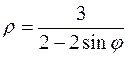
3. а) 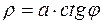 б)
б) 

4. а)  б)
б) 
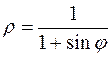
5. а)  б)
б) 

6. а) 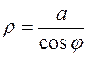 б)
б) 

7. а)  б)
б) 

8. а) 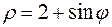 б)
б) 

9. а) 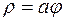 б)
б) 

10. а)  б)
б) 
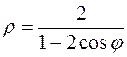
11. а)  б)
б) 

12. а) 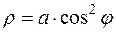 б)
б) 

13. а)  б)
б) 

14. а)  б)
б) 

15. а) 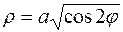 б)
б) 
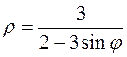
16. а)  б)
б) 

17. а)  б)
б) 
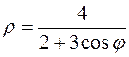
18. а)  б)
б) 

19. а)  б)
б) 
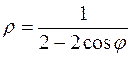
20. а)  б)
б) 
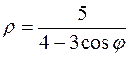
21. а)  б)
б) 

22. а)  б)
б) 

23. а) 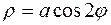 б)
б) 

24. а) 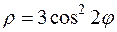 б)
б) 

25. а)  б)
б) 

26. а) 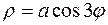 б)
б) 

27. а)  б)
б) 
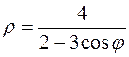
28. а) 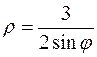 б)
б) 
29. а)  б)
б) 

30. а)  б)
б) 

Задача 6.
1. Объем правильной треугольной призмы равен  . Какова должна быть сторона основания, чтобы полная поверхность призмы была наименьшей?
. Какова должна быть сторона основания, чтобы полная поверхность призмы была наименьшей?
2. Открытый чан имеет форму цилиндра. При данном объеме  , каковы должны быть радиус основания и высота цилиндра, чтобы его поверхность была наименьшей?
, каковы должны быть радиус основания и высота цилиндра, чтобы его поверхность была наименьшей?
3. Из трех тонких одинаковых досок изготовить желоб с наибольшим поперечным сечением.
4. Одна сторона прямоугольного участка земли примыкает к берегу канала, а другие три огораживаются забором. Каковы должны быть размеры этого участка, чтобы его площадь равнялась 800 м2, а длина забора была наименьшей?
5. Из полосы жести шириной 30 см требуется сделать открытый сверху желоб, поперечное сечение которого имеет форму равнобочной трапеции. Дно желоба 10 см. Каков должен быть угол, образованный стенками желоба с дном, чтобы он вмещал наибольшее количество жидкости?
6. В прямоугольной системе координат через точку (1;4) проведена прямая, пересекающаяся с положительными полуосями координат. Написать уравнение прямой, если сумма отрезков, отсекаемых ею на осях координат, принимает наименьшее значение.
7. Стрела прогиба балки прямоугольного сечения обратно пропорциональна произведению ширины этого сечения на куб его высоты. Каковы должны быть размеры сечения балки, вырезанной из круглого бревна диаметром 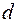 с наименьшей стрелой прогиба?
с наименьшей стрелой прогиба?
8. Сопротивление балки прямоугольного сечения на изгиб пропорционально произведению ширины этого сечения на квадрат его высоты. Каковы должны быть размеры сечения балки из круглого бревна диаметром 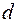 , чтобы ее сопротивление на изгиб было наибольшим?
, чтобы ее сопротивление на изгиб было наибольшим?
9. Окно имеет форму прямоугольника, завершающегося полукругом. Периметр окна равен 300 см. При каких размерах окно будет пропускать наибольшее количество света?
10. Из куска жести, форма и размеры которого (в дм) даны на рис.7, вырезать прямоугольник с наибольшей площадью.
11. При конструировании трансформатора переменного тока важно заполнить внутренность катушки железным крестообразным сердечником возможно большей площади. Каковы должны быть соответствующие размеры  и
и  сечения, если радиус катушки равен
сечения, если радиус катушки равен  .
.
12. Сосуд состоит из цилиндра, заканчивающегося снизу полусферой, он должен вмещать 18 л воды. Найти размеры сосуда, при которых на его изготовление пойдет наименьшее количество материала.
13. Полоса жести шириной 60 см должна быть согнута в виде открытого желоба так, чтобы поперечный разрез имел форму трапеции, причем АС=СД=ДВ. Определить ширину желоба АВ, при которой вместимость его была наибольшей.
14. Требуется изготовить из жести ведро данного объема  цилиндрической формы без крышки. Найти высоту цилиндра и радиус его основания, при которых на ведро уйдет наименьшее количество материала.
цилиндрической формы без крышки. Найти высоту цилиндра и радиус его основания, при которых на ведро уйдет наименьшее количество материала.
15. В данный конус с радиусом основания  и высотой
и высотой 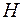 вписать цилиндр наибольшего объема.
вписать цилиндр наибольшего объема.
16. На странице печатный текст должен занимать  кв.см. Верхнее и нижнее поля должны быть по
кв.см. Верхнее и нижнее поля должны быть по  см, правое и левое по
см, правое и левое по 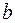 см. Если принимать во внимание экономию бумаги, то какими должны быть наиболее выгодные размеры страницы?
см. Если принимать во внимание экономию бумаги, то какими должны быть наиболее выгодные размеры страницы?
17. Cила действия кругового электрического тока на небольшой магнит, ось которого расположена на перпендикуляре к плоскости круга, проходящем через его центр, выражается формулой  ; где
; где  – радиус круга,
– радиус круга,  – расстояние от центра круга до магнита
– расстояние от центра круга до магнита  ,
, 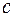 – постоянная. При каком
– постоянная. При каком  величина
величина  будет наибольшей?
будет наибольшей?
18. Определить размеры открытого бассейна с квадратным дном объёмом 32 м3 так, чтобы на облицовку его стен и дна пошло наибольшее количество материала.
19. Требуется изготовить закрытый цилиндрический бак объемом  . Каким должны быть его размеры, чтобы на его изготовление ушло наименьшее количество материала?
. Каким должны быть его размеры, чтобы на его изготовление ушло наименьшее количество материала?
20. Пункт В находится на расстоянии 60 км от железной дороги. Расстояние по железной дороге от А до ближайшей к пункту В точки С составляет 285 км. На каком расстоянии от С надо построить станцию, чтобы затрачивать наименьшее время на передвижение между пунктами А и В, если скорость движения по железной дороге 52 км/ч, а по шоссе 20 км/ч.
21. Найти длины сторон прямоугольника наибольшей площади, вписанного в прямоугольный треугольник с катетами18 см и 24 см и имеющего с ним общий прямой угол.
22. Найти радиус основания 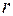 и высоту
и высоту  прямого кругового конуса, вписанного в шар радиуса
прямого кругового конуса, вписанного в шар радиуса  так, чтобы его объём был наибольшим.
так, чтобы его объём был наибольшим.
23. Даны две точки А(0;3) и В(4;5). Найти на положительной полуоси ОX такую точку С, чтобы АС+СВ было наименьшим.
24. В прямоугольный треугольник с гипотенузой 8см и углом 600 вписан прямоугольник, основание которого расположено на гипотенузе. Каковы должны быть размеры прямоугольника, чтобы его площадь была наибольшей?
25. Периметр осевого сечения цилиндра равен 12 м. Найти наибольший объём такого цилиндра.
26. Найти стороны прямоугольника наибольшего периметра, вписанного в полуокружность радиуса  .
.
27. Найти наибольший объём цилиндра, у которого периметр осевого сечения равен 6м.
28. Периметр равнобедренного треугольника равен 2р. Каковы должны быть его стороны, чтобы объём тела, образованного вращением этого треугольника вокруг основания был наибольшим?
29. Полотняный шатер объёмом  имеет форму прямого кругового конуса. Каково должно быть отношение высоты конуса к радиусу основания, чтобы на шатер ушло наименьшее количество полотна?
имеет форму прямого кругового конуса. Каково должно быть отношение высоты конуса к радиусу основания, чтобы на шатер ушло наименьшее количество полотна?
30. Найти отношение радиуса цилиндра к высоте, при котором цилиндр при данном объёме  имеет наименьшую полную поверхность.
имеет наименьшую полную поверхность.
ЗАКЛЮЧЕНИЕ
Если функциональная зависимость дана в виде формулы y = f(x), то каждой паре значений величин х и у соответствует определенная точка плоскости, т. е. каждому значению х отвечает определенное значение у. Если нанести на график несколько точек, то промежуточные точки и весь график можно получить, соединяя плавной линией нанесенные точки. Но для того чтобы не сделать при этом грубых ошибок, нужно иметь общее представление о виде кривой.
В данном пособии рассмотрены основные этапы исследования функции (нахождение максимумов и минимумов, асимптот, точек перегиба) и построение графиков.
Текстовые задачи, в которых надо записать функцию и исследовать ее на экстремум, представляют один из видов задач оптимизации (при наименьших расходах требуется получить наибольший эффект).
Изучение методов исследования и выполнение предложенных заданий, позволит студенту грамотно оценить и проанализировать те зависимости между величинами, с которыми он неминуемо встретится и при дальнейшем обучении, и в своей профессиональной деятельности.
Дата добавления: 2015-10-26; просмотров: 867 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ПРИМЕРЫ ИССЛЕДОВАНИЯ ФУНКЦИЙ И ПОСТРОЕНИЯ ГРАФИКОВ | | | Deep within the Alps, mortal realm |