
Читайте также:
|
В данном разделе рассмотрены задачи, связанные с исследованием функций и построением их графиков. Примеры даны с подробным решением. Приступая к выполнению типового расчета, студент может рассмотреть соответствующий пример данного раздела и найти ответы на возникающие при работе вопросы.
Пример 1. Найти асимптоты кривой 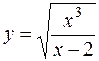 и построить график функции по точкам.
и построить график функции по точкам.
Решение.
1. Поскольку корень четной степени принимает только арифметические значения, то график функции целиком расположен выше оси ОХ. Функция определена при условии 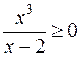 , т.е. в интервалах
, т.е. в интервалах 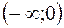 и
и 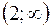 . Поэтому исследуем поведение функции при
. Поэтому исследуем поведение функции при 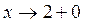 и
и  .
.
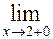
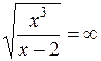 , значит прямая х = 2 является вертикальной асимптотой.
, значит прямая х = 2 является вертикальной асимптотой.
Теперь рассмотрим поведение функции слева от нуля: 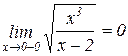 . Мы получили конечный предел, поэтому прямая
. Мы получили конечный предел, поэтому прямая  не является вертикальной асимптотой. По мере приближения к точке
не является вертикальной асимптотой. По мере приближения к точке  слева функция стремится к нулю, оставаясь при этом положительной.
слева функция стремится к нулю, оставаясь при этом положительной.
2.Определим уравнения невертикальных асимптот.
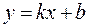 при
при 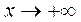 и
и  .
.
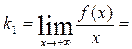

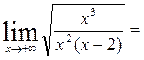
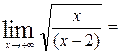 1;
1; 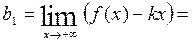
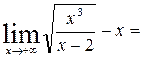
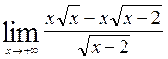 = =
= = 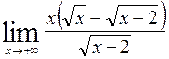 =
= 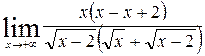 = =
= =  =
= 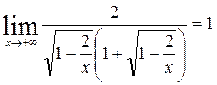 .
.
Таким образом, существует правая наклонная асимптота  .
.
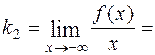
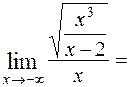
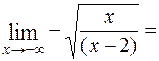 -1;
-1;
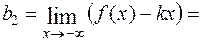
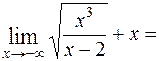
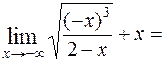 =
= 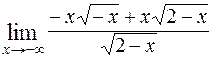 =
=  = =
= = 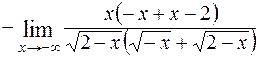 =
=  .
.
Существует левая наклонная асимптота 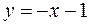 .
.
Для построения графика необходимо взять несколько дополнительных точек:
| Х | -1 | -2 | 2,5 | |||
| у | 0,58 | 1,4 | 5,6 | 5,2 | 5,6 |
График функции изображен на рис. 1.
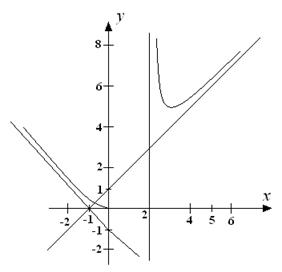
Рис.1. График функции 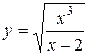 .
.
Пример 2. Провести полное исследование функции 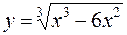 и построить ее график.
и построить ее график.
Решение.
1. Область определения функции:  .
.
2. Точек разрыва нет, так как функция существует при любых действительных значениях  .
.
3. Найдем асимптоты:
а) вертикальных асимптот нет, так как нет точек разрыва второго рода;
б) невертикальные асимптоты (в данном примере исследования при 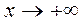 и
и  аналогичны):
аналогичны):
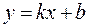
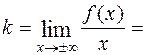

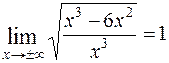 ;
;
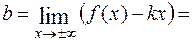
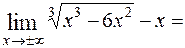 =
= 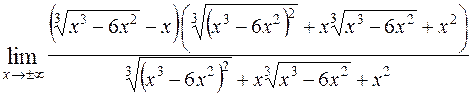 = =
= = 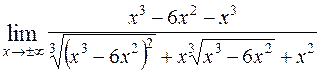 = =
= = 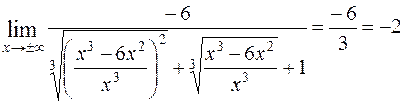 .
.
Уравнение невертикальной асимптоты 
4. Исследование на экстремум
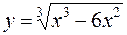
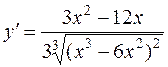 =
=  =
=  ;
;
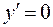 при
при 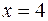 . Производная не существует при
. Производная не существует при 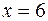 и
и 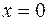 .
.
Составим таблицу:
| х | 
| (0;4) | (4;6) | (6;+∞) | |||

| + | Не сущест. | ─ | + | Не сущест. | + | |
| у | возрастает | max | убывает | min | возрастает | возрастает |
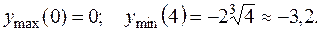
5. Исследование на перегиб
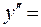
 =
=
= 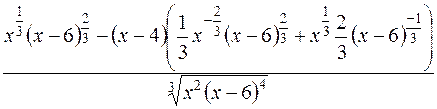 = =
= = 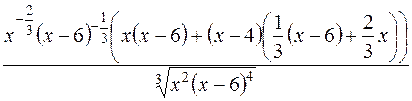 = =
= = 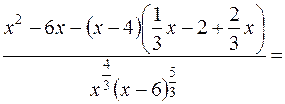
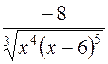 .
.
Вторая производная при любых  отлична от нуля и не существует при
отлична от нуля и не существует при 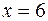 и
и 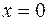 .
.
Составим таблицу:

| 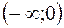
| 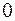
| 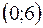
| 
| 
|

| + | Не сущ. | + | Не сущ. | - |
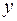
| Вогнута | Нет точек перегиба | Вогнута | Точка перегиба | Выпукла |
Значение функции в точке перегиба 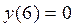 .
.
6. Точки пересечения с осями координат.
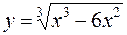 =
= 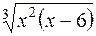
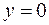 при
при 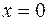 и
и 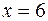 .
.
7. По данным исследования строим график функции (рис. 2).

Рис. 2. График функции  .
.
Пример 3. Провести полное исследование функции 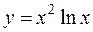 и построить её график.
и построить её график.
Решение.
1. Область определения функции: 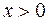
2. Исследуем граничную точку 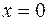 .
.
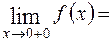

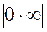 =
= 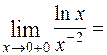
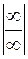 =
= 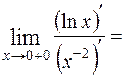
= 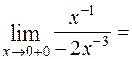
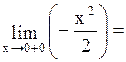
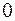 .
.
3. Заметим, что функция в окрестности точки 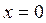 стремится к нулю, оставаясь при этом отрицательной. Конечный предел означает, что вертикальных асимптот нет. Находим невертикальные асимптоты
стремится к нулю, оставаясь при этом отрицательной. Конечный предел означает, что вертикальных асимптот нет. Находим невертикальные асимптоты 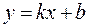 .
.
Так как функция определена при 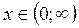 , то исследуем ее поведение лишь при
, то исследуем ее поведение лишь при 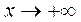 .
.
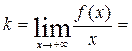
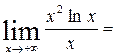
 .
.
Невертикальных асимптот нет.
4. Исследование на экстремум
 ;
;
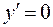 ,
, 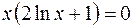 при
при 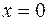 или
или 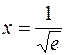 , причем
, причем 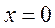 ─ граничная точка области определения.
─ граничная точка области определения.
Составим таблицу:

| 
| 
| 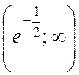
|
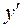
| – | + | |
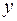
| Функция убывает | - 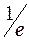 (min) (min)
| Функция возрастает |
5. Определим интервалы выпуклости и вогнутости кривой. Найдем точки перегиба
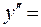
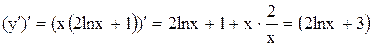 .
.
Производная обращается в ноль при 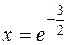 .
.
Составим таблицу:

| 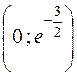
| 
| 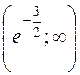
|

| - | + | |
| выпукла | точка перегиба | вогнута |
 =
= 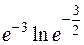
 .
.
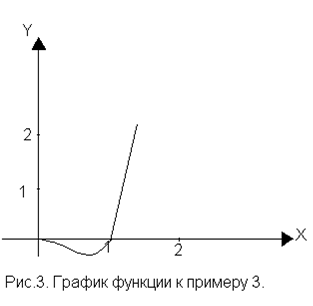
График функции изображен на рис. 3.
Пример 4. Исследовать функцию и поострить её график
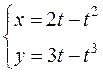 .
.
Замечание. При исследовании функций, заданных параметрически, можно пользоваться упрощенной схемой исследования.
1. Найти область изменения переменных 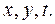
2. Найти точки пересечения графика с осями координат.
3. Найти производную функции и точки, в которых она обращается в нуль или не существует. Учитываем, что в точках, где производная равна нулю, касательная к графику параллельна оси ОХ, а в точках, где производная не существует, касательная перпендикулярна оси ОХ.
4. При необходимости взять несколько дополнительных точек.
Решение.
Поскольку х и у выражены через параметр t, то можно получить соответствующие значения х и у. Таким образом, построение функции, заданной параметрически, удобнее всего проводить поточечно, если есть возможность вычислить достаточно большое число точек.
1. Рассмотрим первоначально 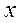 и
и  как функции от
как функции от 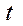 . В системе координат
. В системе координат 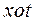 выражение
выражение 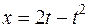 определяет параболу, переменная
определяет параболу, переменная 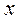 определена при любом
определена при любом 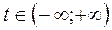 , причем при
, причем при 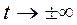 переменная
переменная  . Максимальное значение
. Максимальное значение 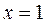 соответствует значению
соответствует значению 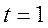 (вершина параболы), следовательно
(вершина параболы), следовательно 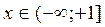 . Для функции
. Для функции 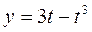 максимального значения не существует. Функция определена при
максимального значения не существует. Функция определена при 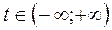 и
и 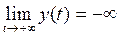 ,
, 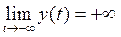 ,
, 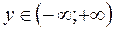 .
.
2. Точки пересечения с осями координат.
Если 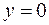 , то
, то  , то
, то 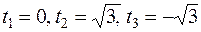 . Этим значениям
. Этим значениям 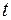 соответствуют следующие значения
соответствуют следующие значения  :
:  . Это точки пересечения графика с осью ОХ.
. Это точки пересечения графика с осью ОХ.
Если 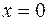 , то
, то 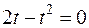 ,
, 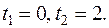 Этим значениям
Этим значениям 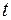 соответствуют следующие значения
соответствуют следующие значения 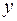 :
: 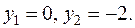 Это точки пересечения с осью ОУ.
Это точки пересечения с осью ОУ.
3. Вычислим производную и определим экстремум функции и интервалы монотонности: 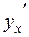 =
= 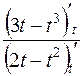 =
= 
Заметим, что при  производная
производная 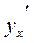 не определена. На графике параметру
не определена. На графике параметру  соответствует точка с координатами
соответствует точка с координатами 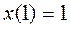 ,
, 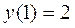 , точка (1;2). В окрестности точки
, точка (1;2). В окрестности точки  производная
производная  положительна, что соответствует монотонному возрастанию функции.
положительна, что соответствует монотонному возрастанию функции.
Производная  при
при  , что соответствует точке (-3;-2). В этой точке касательная к графику функции параллельна оси ОХ, а точка (-3;-2) является точкой минимума, поскольку производная при переходе через точку
, что соответствует точке (-3;-2). В этой точке касательная к графику функции параллельна оси ОХ, а точка (-3;-2) является точкой минимума, поскольку производная при переходе через точку  меняет знак с «-» на «+».
меняет знак с «-» на «+».
4. Вторая производная позволит выяснить направление выпуклости графика функции: 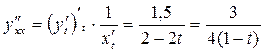 . Поскольку
. Поскольку  при
при 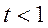 , то функция выпукла вниз (вогнута), а при
, то функция выпукла вниз (вогнута), а при 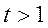 график функции направлен выпуклостью вверх, так как
график функции направлен выпуклостью вверх, так как  .
.
5. Можно взять дополнительные точки и нарисовать график функции (рис. 4):
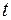
| -1 | ||

| -3 | ||
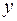
| -2 | -18 |
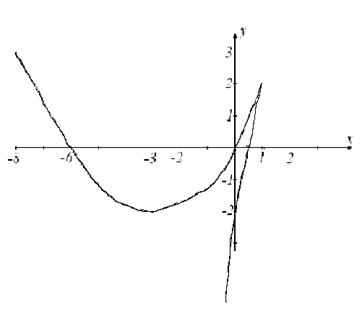
Рис. 4. График функции  .
.
Дата добавления: 2015-10-26; просмотров: 306 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| КОММЕНТАРИИ К ОБЩЕЙ СХЕМЕ ИССЛЕДОВАНИЯ ФУНКЦИЙ | | | ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ГЕОМЕТРИЧЕСКОГО И ФИЗИЧЕСКОГО СОДЕРЖАНИЯ |