Комментарии к общей схеме исследования функций

1. При нахождении области определения и непрерывности функции следует вспомнить основные свойства известных из школьной программы элементарных функций:

а) степенная функция , , определена при условии ;

б) рациональная функция 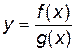определена при условии ;

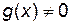в) иррациональная функция в случае четного n определена при условии . Если же n нечетно, то область определения функции совпадает с областью определения функции ;

г) показательная функция имеет ту же область определения, что и ;

д) логарифмическая функция определена при ;

е) тригонометрические функции , определены для . Функция не определена в случае , , 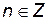а функция не определена для , ;

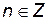ж) обратные тригонометрические функци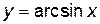и и 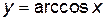определены только на отрезке [-1, 1], а функции и существуют при .

Следует также помнить, что элементарные функции непрерывны в области определения.

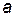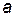2. Дополнительные условия в некоторых случаях позволяют значительно упростить построение графика. Прежде всего, надо вспомнить о правилах, по которым выполнялись построения в школе. Если известен график функции , то график получается сдвигом графика на единиц по оси ОХ. График – сдвигом на единиц по оси OY. График означает сжатие или растяжение графика по оси ОХ. График получается из графика изменением ординаты в раз. Эти простые правила значительно упрощают построение. Например, чтобы построить график функции достаточно провести преобразования и заметить, что график данной функции может быть получен из графика гиперболы сдвигом последнего на единицу влево по оси ОХ и на единицу вверх по оси OY.

Проверка четности или нечетности функции позволяет, используя симметрию, исследовать только поведение функции для x>0. Напомним, что четной называется функция , определенная на симметричном относительно х=0 промежутке и обладающая свойством 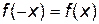. График чётной функции симметричен относительно оси OY (осевая симметрия). Функция называется нечётной, если она определена на симметричном относительно х = 0 промежутке и . График нечетной функции симметричен относительно начала координат (центральная симметрия).

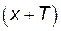Рассматривая вопрос периодичности той или иной функции, следует помнить, что среди элементарных функций свойством периодичности, при действительной переменной, обладают только тригонометрические функции. Периодом функции называется число такое, что при любом из области определения числа и 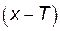также принадлежат области определения функции и . Числа , где n – любое натуральное число, также являются периодами функции . У функции любое число будет периодом. Если функция f(x) имеет период Т, то функция , имеет период . Например, функция имеет период , а функция имеет период . Для получения графика периодической функции достаточно построить график на любом промежутке длины Т: и переместить эту часть графика вдоль оси ОХ на . Если периодическая функция имеет производную, то 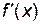является периодической функцией с тем же периодом.

Наконец, дополнительные точки, а именно точки пересечения с осями координат, в начале исследования нужно находить лишь в случае, когда эти значения практически очевидны (т. е. не требуют излишних вычислительных усилий).

3. Наличие асимптот у графика функции значительно упрощает построение. Существование асимптот означат, что при достаточном удалении от начала координат ( или 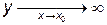) функция ведет себя почти как линейная, то есть отличается от линейной на бесконечно малую. Асимптота – это прямая, расстояние до которой от графика функции стремится к нулю по мере удаления от начала координат. Различают асимптоты вертикальные (параллельные оси ОУ) и наклонные или горизонтальные (непараллельные оси ОУ):

а) наличие вертикальных асимптот определяется при исследовании характера точек разрыва или на границе области определения функции. Пусть функция y = f(x) определена в некоторой окрестности точки 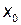(окрестность может быть односторонней) и выполнено одно из условий или , тогда прямая является вертикальной асимптотой графика функции. Заметим, что если , где и 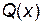многочлены, и , , 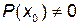то прямая является асимптотой графика функции;

б) уравнение невертикальной асимптоты , где и − некоторые числа, определяется из условия . Причем исследования при и проводятся отдельно. Числа и находятся по формулам ; . Если указанные пределы не существуют (т. е. нет конечных пределов), то невертикальных асимптот нет.

4. После нахождения асимптот надо попытаться примерно построить график функции, учитывая уже проведенные исследования, т. е. указать точки пересечения кривой с осями координат, нарисовать асимптоты, учесть симметрию, если таковая существует, изобразить схематически график функции. Очень часто полученный вид не претерпевает существенных изменений при дальнейших исследованиях.

5. Вычисление первой и второй производных позволит найти интервалы монотонности, точки экстремума, промежутки выпуклости графика, точки перегиба.

6. Точки, в которых первая производная равна нулю или не существует, называются критическими. Если функция дифференцируема в точке , имеет в этой точке максимум или минимум, то .

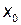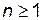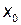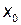Для нахождения максимумов и минимумов можно использовать производные высших порядков. Пусть в точке у функции существуют производные до порядка включительно. Причем все производные порядка меньшего равны нулю в точке , а производная порядка отлична от нуля, , , …, , . Тогда если − четное число, то функция имеет в точке экстремум, а именно максимум, если , и минимум, если . 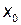Если же − нечетное число, то функция не имеет в точке экстремума. 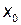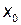В этом случае, при точка является точкой возрастания, а при точка − точка убывания функции.

7. Определив все критические точки, в которых либо , либо 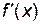не существует, надо расположить эти точки, а также точки разрыва функции на оси абсцисс в порядке возрастания. Внутри полученных интервалов установить знак первой производной. Если на интервале , то функция на этом промежутке возрастает, если , то функция убывает. Если знак производной при переходе через критическую точку изменяется (при условии, что функция в этой точке определена), то в точке экстремум. Если 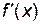меняет знак с «–» на «+», то критическая точка является точкой минимума, если с «+» на «–», то критическая точка является точкой максимума. Если смены знака не происходит, то экстремума нет.

В точках экстремума необходимо вычислить значение функции и изобразить эти точки на графике. Следует помнить, что условие означает, что в точке 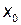касательная к графику функции параллельна оси ОХ (гладкий экстремум), если же в точке экстремума производная не существует, то гладкость графика нарушается и экстремум имеет форму пика.

8. Нахождение точек, в которых вторая производная обращается в нуль или не существует, позволяют определить точки перегиба графика функции. Если функция f(x) имеет непрерывную вторую производную в точке 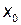, и эта точка является точкой перегиба графика функции f(x), то . Для нахождения точки перегиба можно воспользоваться достаточным условием, требующим вычисления третьей производной. Пусть , а , тогда 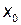является точкой перегиба.

9. Точки, в которых вторая производная либо равна нулю, либо не существует, а также точки разрыва функции расположить в порядке возрастания на оси абсцисс. Внутри полученных интервалов установить знак второй производной. Если на интервале , то функция на этом промежутке строго выпукла вверх. Если на интервале , то функция строго выпукла вниз (вогнута). Если знак второй производной при переходе через критическую точку изменяется (при условии, что функция в этой точке определена), то данная точка является точкой перегиба.

В точках перегиба необходимо вычислить значение функции и изобразить эти точки на графике.

10. Результатом проведенного исследования является построение графика функции. Построение должно проводиться по мере исследования, т. е. каждый шаг должен приносить некоторые изменения и дополнения к рисунку, уже полученному на предыдущем этапе: точки разрыва, точки пересечения с осями, асимптоты, точки экстремума, промежутки монотонности, точки перегиба, интервалы выпуклости. Обычно этих данных бывает достаточно для построения графика. Если требуются какие-либо уточнения, то можно вычислить несколько дополнительных точек.

Дата добавления: 2015-10-26