Общая схема исследования функций и построения графиков

ББК В 161.11я73

© ГОУ ВПО «Дальневосточный государственный
университет путей сообщения» (ДВГУПС), 2006

ВВЕДЕНИЕ

Целью изучения математики в техническом или экономическом вузе является возможность применения полученных знаний к исследованию реальных явлений в технике, физике, социальных и экономических науках.

При рассмотрении того или иного явления часто встречаются зависимости одних величин от других – функциональные зависимости. Функциональная зависимость одной величины 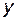от другой означает, что каждому значению соответствует определенное значение 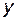. Величина при этом называется независимой переменной или аргументом, а 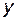– функцией этой переменной. В математике функциональная зависимость чаще всего задается формулами, которые дают способ вычисления значения функции при каждом заданном значении независимой переменной.

В данной разработке рассматриваются функции, зависящие только от одной действительной переменой: 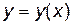. Такую функцию можно наглядно представить на плоскости в виде графика в декартовых или полярных координатах. Каждой паре значений отвечает на координатной плоскости одна точка. Самый примитивный способ построения графика функции 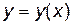– это построение по точкам. Но для точного представления понадобится вычислить довольно большое число значений пар . Такой способ не экономичен. Кроме того, можно пропустить точки, в которых происходит резкое изменение поведения функции. Гораздо быстрее и надежнее построить график, позволяющий составить общее представление о виде кривой. Для этого понадобятся некоторые знания математического анализа.

В данном методическом пособии рассматриваются основные методы исследования функций и построения графиков с использованием дифференциального исчисления.

Пособие предназначено для студентов первого курса всех специальностей, изучающих математику.

ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИЙ И ПОСТРОЕНИЯ ГРАФИКОВ

График функции позволяет установить важные сведения о функции, например, узнать число вещественных корней уравнения 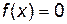, найти промежутки, в которых располагаются корни, получить информацию о максимумах и минимумах и т.д.

Построение графика функции целесообразно проводить в следующем порядке.

1. Найти область определения функции, область непрерывности и точки разрыва.

2. Проверить выполнение некоторых дополнительных условий, помогающих построению (периодичность, чётность, нечётность, точки пересечения графика с осями координат).

3. Найти асимптоты графика функции.

4. Приблизительно, на черновике, нарисовать график функции.

5. Вычислить первую и вторую производные.

6. Найти точки, в которых первая производная либо не существует, либо равна нулю.

7. Составить таблицу изменения знака первой производной. Определить промежутки возрастания, убывания функции. Найти точки экстремума.

8. Найти точки, в которых вторая производная либо не существует, либо равна нулю.

9. Составить таблицу изменения знака второй производной. Определить промежутки выпуклости вверх или вниз графика функции, найти точки перегиба.

10. Окончательно вычертить график, используя все полученные результаты.

Для более точного построения графика можно вычислить ещё какие-либо дополнительные точки по мере потребности.

Если вторая производная имеет очень громоздкие выражения, то иногда приходиться ограничиваться свойствами графика, которые можно установить с помощью первой производной.

Схема исследования, предложенная здесь, может несколько изменяться в каждом конкретном случае. Например, можно менять местами шаги исследования.

Дата добавления: 2015-10-26