Тема 7. Индексы

При изучении содержания темы студент должен составить представление об индексе как показателе сравнения двух величин; элементах, входящих в построение индексов; различиях индексов индивидуальных и агрегатных, индексов объемных и качественных показателей.

Основное внимание должно быть уделено агрегатным индексам – показателям сравнения характеристик сложных явлений, состоящих из непосредственно не суммируемых элементов.

Надо усвоить методику построения агрегатных индексов физи­ческого объема продукции. Следует иметь в виду, что основной проблемой при построении этих индексов является проблема выбора показателей-соизмерителей, обеспечивающих сопоставимость числителя и знаменателя индекса.

Индексируемые показатели, а также явления, выступающие в роли соизмерителей, могут быть качественными и количественными (объемными). Количественные показатели представляют собой численность тех или иных еди­ниц или общий объем какого-либо признака. Качественные характеризу­ют уровень явления в расчете на ту или иную единицу совокупности.

При построении агрегатных индексов качественных показателей в роли соизмерителей выступают количественные показатели и фиксируются на уровне отчетного периода. При построении агрегатных индексов количественных показателей в роли соизмерителей выступают качественные показатели и фиксируются на уровне базисного периода.

Индивидуальные индексы не требуют соизмерителей, т.к. при их расчете сравниваются абсолютно однородные явления:

, , , и т.п., (7.1)

где q – количество единиц продукции одного вида (шт., т, л,...);

p – цена единицы определенного вида продукции (руб.);

z – себестоимость единицы определенного вида продукции (руб.);

w – производительность труда одного человека (шт., т, л,...).

Средние индексы (арифметический, гармонический) студент изучает в связи с агрегатными. Агрегатные индексы качественных показателей применяются в двух формах: в форме индексов перемен­ного состава и в форме индексов фиксированного состава.

Индекс среднего уровня может быть представлен как произведение аналитических индексов-сомножителей, каждый из которых отражает изменение только одного фактора, и тем самым – влияние этого изменения на динамику среднего уровня. Первый индекс носит название индекса фиксированного состава, второй – индекса структурных сдвигов.

(7.2)

Например, для анализа динамики среднемесячной производительности труда (w) по группе работников индекс переменного состава определяется по формуле:

,

(7.3)

где , – стоимость произведенной продукции в отчетном и базисном периодах в сопоставимых ценах;

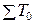, – численность работников в отчетном и базисном периодах. Индекс фиксированного состава:

, (7.4)

где – индивидуальные индексы производительности труда.

Индексы, приведенные в формуле (7.4), являются индексами фиксированного состава, т.к. в каждом из них индексируется только одна величина; напротив, индексы, приведенные в формуле (7.3), характеризуют изменение и качественных величин (w), и структуры количественных (T).

Эта структура может быть выражена в виде относительных величин:

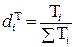(7.5)

В дальнейшем, для отражения отличия структуры показателя Т (либо других количественных показателей) в разных условиях, будет применяться обозначение 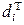. В других индексах могут использоваться показатели 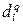, и т.д.

Индексные методы широко применяются для анализа факторов изменения сложных показателей, полученных на основе соизмерения абсолютных величин. В связи с этим необходимо изучить вопрос о способах построения взаимосвязанных индексов и способах расчета абсолютного изменения сложной величины за счет влияющих факторов.

Индекс результативного показателя связан с индексами показателей-факторов так же, как абсолютные величины этих показателей:

, (7.6)

где 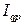– индекс стоимости продукции;

– индекс физического объема продукции в базисных ценах;

– индекс цен.

Такая взаимосвязь может быть использована не только для выявления относительного изменения уровня изучаемого явления за счет отдельных факторов, но и для определения размера абсолютного изменения уровня сложного явления в связи с влиянием исследуемых факторов:

. (7.6а)

Среди наиболее часто используемых в экономических расчетах индексов необходимо отметить:

индексы объема

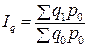, ; (7.7)

индексы цен

, ; (7.8)

индексы себестоимости

, . (7.9)

Индексы производительности труда могут иметь три формы:

натуральные

, ; (7.10)

стоимостные

, ,

; (7.11)

трудовые

, ,

, (7.12)

где t – трудоемкость изготовления единицы продукции.

Индексы заработной платы также имеют две формы (индивидуальный индекс и сводный индекс), т.к. заработная плата – это сумма, начисленная в счет оплаты за работу одного человека, т.е. показатель качественный:

, ,

, (7.13)

где Ф – фонд заработной платы всех работников на исследуемом объекте,

f – заработная плата одного работника.

В выше приведенных формулах использованы условные обозначения любого учебника «Общей теории статистики».

Завершая изучение темы, следует обратить внимание на наличие взаимосвязей между следующими группами индексов:

- индивидуальными и сводными;

- индексами базисными и цепными;

- индексами переменного и фиксированного состава;

- индексами взаимосвязанных явлений.

Дата добавления: 2015-10-26