Читайте также:
|
Проработку темы следует начать с выяснения сущности и задач используемых на практике форм несплошного наблюдения. Необходимо затем уяснить природу ошибки выборочного наблюдения (ошибки репрезентативности) и усвоить, что репрезентативность несплошного наблюдения может быть обеспечена лишь при правильной организации отбора подлежащих обследованию единиц. Важно четко представить себе особенности и преимущества выборочного наблюдения по сравнению с другими разновидностями несплошного наблюдения, уяснить смысл понятия «случайный отбор» и значение принципа случайного отбора для обеспечения репрезентативности результатов наблюдения.
Студент должен ознакомиться также с различными формами организации выборочного наблюдения. Выборочное наблюдение опирается на закон больших чисел и относящиеся к этому закону теоремы, которые используются при оценке результатов выборки. Необходимо познакомиться с использованием этого материала и усвоить формулы для расчета средних и предельных ошибок доли исредней величины признака (при различных формах организации выборки) и определения числа единиц выборочной совокупности, необходимой для обеспечения заданной точности результата. Формулы необходимо усвоить практически, путем решения приведенных в учебниках и учебных пособиях задач.
При решении задач следует использовать общепринятые условные обозначения, которые приведены ниже.
| Показатели | Обозначения в совокупностях | |
| генеральной | выборочной | |
| Число единиц | N | n |
| Средняя величина | 
| 
|
| Число единиц, обладающих изучаемым признаком | M | m |
| Доля единиц, обладающих изучаемым признаком | 
| 
|
| Доля единиц, не обладающих изучаемым признаком | 
| 
|
| Дисперсия | 
| 
|
| Средняя ошибка | – |  , 
|
| Предельная ошибка | – |  ,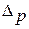 
|
Различие (отклонение) между генеральной средней и выборочной средней, между генеральной долей единиц, обладающих изучаемым признаком, и соответствующим выборочным показателем называется ошибкой выборки, которая зависит от колеблемости признака в совокупности и численности единиц выборки.
При изучении среднего значения признака средняя ошибка вычисляется по формулам:
для повторного отбора
, (8.1)
для бесповторного
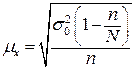. (8.2)
Предельная ошибка отличается введением в эти формулы коэффициента доверия (Стъюдента), который зависит от гарантируемой вероятности точности результатов:
(8.3)
При определении доли единиц, обладающих изучаемым признаком, аналогичные формулы записываются следующим образом:
для повторного отбора
, (8.4)
для бесповторного отбора
. (8.5)
Предельные ошибки вычисляются с введением коэффициента доверия
. (8.6)
Подсчитав отклонения выборочных показателей от генеральных и все характеристики выборочной совокупности, можно подсчитать генеральные показатели:
, (8.7)
. (8.8)
Если допустимая ошибка выборки или 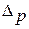задана, то можно подсчитать, какое число единиц выборочной совокупности необходимо подвергнуть наблюдению, чтобы не превысить заданную величину ошибки. Для этого определяют n из формул (8.3) или (8.6).
Дата добавления: 2015-10-26; просмотров: 70 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тема 7. Индексы | | | Тема 9. Методы статистического изучения взаимосвязи |