Особливості аналізу АМЗ

Основну особливість в розрахунок таких машин вносить факт, що глибина проникнення вихрових струмів та потоку у феромагнітний масив ротора , в значній мірі залежить від частоти зміни цих струмів . Так, наприклад, при великих частотах f в роторі (початок пуску – ) D=2 мм, а при малих частотах (робочий режим ) D=(1¸2) см. Витіснення струмів і потоку ротора на його зовнішню поверхню при великих частотах називають поверхневим ефектом.

Рис. 4. Розподіл силових ліній потоків розсіяння ротора Ф_s2

в його феромагнітному масиві

Дещо спрощено поверхневий ефект можна пояснити значними потоками розсіяння Ф_s2 вихрових струмів феромагнітного масиву ротора. Якщо виділити в цьому масиві елементарний стрижень – “активний провідник обмотки” ротора (рис. 4), то як випливає з цього рисунку для нижніх його волокон потокозчеплення зі “своїми” потоками Ф_s2-y_Фs2 є більшим від потокозчеплення y_Фs2 верхніх волокон. Тому сумарна ЕРС нижніх волокон “стрижня” е_снв є менша від відповідної ЕРС його верхніх волокон е_свв

(5)

де – ЕРС у волокнах “стрижня” ротора, індукована основним потоком машини Ф₀. Крім цього індуктивний опір розсіяння нижніх волокон “стрижня” . В результаті цих обставин густина струму верхніх волокон “стрижня” є більша, а в нижніх – менша. І ця різниця є тим істотніша, чим вищою є частота струмів ротора, що по суті і спричиняє поверхневий ефект. Цей поверхневий ефект підсилюється ще додатково поверхневим ефектом витіснення основного магнітного потоку Ф₀ в напрямі до повітряного проміжку машини внаслідок чого зменшується магнітна провідність шляхів цього потоку у нижніх волокнах. Таким чином внаслідок поверхневого ефекту при зміні частоти обертання ротора n (w, s) істотно змінюється глибина проникнення струмів і потоків ротора D, в масив, а разом з нею змінюються параметри ротора – активний та індуктивний опори. Глибина проникнення хвилі струму по осі y (див. координатні осі ротора на рис. 4) і, залежні від неї величини опорів ротора та визначаються з рівнянь Максвела, які в Декартовій системі координат ротора x,y,z мають вигляд

(6)

З метою спрощення розрахунків приймають, що магнітне поле в роторі плоскопаралельне, напруженість H (x, y) магнітного поля ротора, індукція цього поля, напруженість електричного поля та густина струму є синусоїдними функціями з частотою зміни ; ( – довжина розгортки дуги ротора); магнітна проникність масиву m є сталою; довжина ротора , тобто струми ротора протікають в основному в аксіальному напрямі.

Систему рівнянь (6) перетворимо так, щоби отримати рівняння вищого порядку, але з однією змінною, наприклад . В результаті перетворень отримуємо

(7)

Розв’язок цього рівняння для нашого випадку, як відомо, необхідно шукати у формі

(8)

Якщо цей розв’язок (8) підставити в останню рівність (7), то отримуємо

звідкіля знайдемо

(9)

або

(10)

Подібно з (6) можна визначити інші невідомі [Постн. стр. 581-582].

Знаючи глибину проникнення в масив D, або густину струму Z, можна обчислити зведений активний опір ротора

(11)

де p – кільлість пар полюсів; k_b – коефіцієнт, що враховує опір “лобових з’єднань” обмотки ротора.

Більш детально визначення див [Постн. c. 582–584]. Величина опору ротора в заступній схемі АМ

(12)

Враховуючи (10) можна обчислити повний опір ротора

(13)

якщо не враховувати зміни магнітної проникності m масиву та втрат на гістерезис при зміні ковзання. Якщо ж це враховувати, то наближено

.

(14)

Але магнітна проникність m феромагнітного масиву ротора залежить від густини струму ротора. Врахувати зміну m при розрахунку таких машин можна застосовуючи метод послідовних наближень, задавшись величиною m при очікуваному струмі ротора і після розрахунків з використанням заступної схеми машини проводити відповідні корекції прийнятих величин, або методом викладеним в [Постн. с. 585].

Знаючи параметри заступної схеми машини, можна, використовуючи її, обчислити характеристики АМ [Постн. с. 587].

В АМ з МФР призначених для роботи в агресивних середовищах, обмотку статора захищають масивним немагнітним екраном (рис. 1, а; див. екран). Щоб зменшити втрати на вихрові струми, в екрані його виконують з матеріалу з великим питомим електричним опором і незначною магнітною проникністю. Глибина проникнення електромагнітної хвилі через такий екран – достатньо велика і хвиля свобідно проходить через екран в ротор. На заступній магнітній схемі машини екран слід розглядати як додатковий магнітний опір Z_ме, якому в електричній заступній схемі машини відповідає електричний опір Z_е, що вмикається паралельно електричному опорові Z_м вітки намагнічування (рис. 5). Складові цього опору Z_е немагнітного екрану визначаються подібно, як для загальмованого НПР (S_е=1).

4. Особливості конструкцій та розрахунку лінійного асинхронного двигуна.

Лінійний асинхронний двигун (ЛАД) – це, як правило асинхронний двигун з масивним ротором – бігуном, який може бути феромагнітним або немагнітним (див. рис. 5 відповідно виконання б) та а), в)).

ЛАД можна подумки представити як розгортку АД циліндричного виконання (див. рис. 5, г). У випадку немагнітного бігуна статор повинен мати двобічний магнітопровід, який може бути обмотаний з обох (рис. 5, а) або тільки з одного боку (рис. 5, в).

Статор ЛАД утворює біжне електромагнітне поле, яке взаємодіючи з вихровими струмами бігуна, утворює тягове зусилля F, яке спричиняє поступальний рух бігуна за полем. Звичайно довжина бігуна більша від довжини статора, або навпаки, з таким розрахунком, щоби тягове зусилля двигуна в межах ходу бігуна було постійним. Якщо масив, в якому утворюються вихрові струми, закріпити, то поступальний рух буде виконувати магнітопровід з обмоткою.

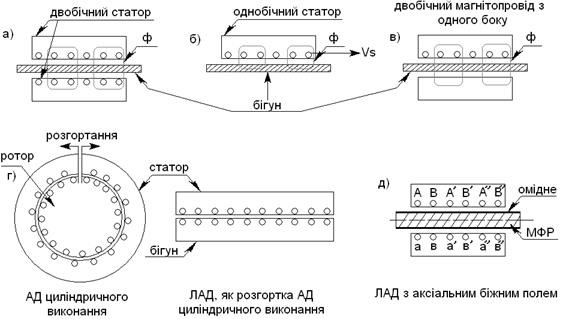
Рис. 5. Конструкційні виконання ЛАД

В багатьох механізмах шлях бігуна обмежується, а його рух тоді є зворотньо-поступальним. Реверсу досягають зміною чергування фаз обмотки статора в кінці шляху, що приводить до реверсування біжного поля. Такі ЛАД виконують з критичним ковзанням S_кр ® 1, і номінальним ковзанням S_н » 0,1 ¸ 0,3.

В ЛАД, показаних на рис. 5, а, б, в, г біжна хвиля електромагнітного поля, а за нею і бігун переміщаються перпендикулярно до напряму активних сторін котушок і тому такий ЛАД називають машиною з поперечним магнітним полем. Якщо цей ЛАД знову згорнути в циліндр, але так, щоби активні сторони котушок обмотки статора уклалися у витки нової обмотки, яка стає гвинтовою m – фазнозахідною обмоткою (див. рис. 5, г), то така обмотка теж утворить біжне поле, напрям переміщення якого збігається з віссю котушок нової обмотки. Асинхронні ЛАД двигуни такої конструкції виконання називають ЛАД з аксіальним полем.

Лінійну швидкість переміщення біжного поля ЛАД V₃ можна обчислити

, (15)

а ковзання ЛАД

S= , (16)

ДеV – лінійна швидкість бігуна; t – полюсний поділ біжної хвилі поля.

Тягове зусилля ЛАД F визначається за виразом

, (17)

де Me –величина електромагнітного моменту АМ, обчислена подібно, як для еквівалентного циліндричного виконання на основі заступної її схеми.

Основною особливістю фізичних явищ в ЛАД є наявність кінцевих ефектів, які виникають внаслідок розриву магнітного кола машини на її кінцях. Магнітні провідності крайніх секцій обмотки менші ніж середніх. Обмотка машини стає якби несиметричною, і як в? машині крім прямобіжної основної хвилі появляються додаткові біжні хвилі поля, які можуть істотно зменшити її тягове зусилля.

Особливості розрахунку ЛАД розглянемо на прикладі двигуна з поперечним полем та з немагнітним бігуном, який має двобічний короткий статор. Модель цієї машини наведена на рис.6.

Рис.6. Модель ЛАД з поперечним полем та з немагнітним бігуном

Користуючись цією моделлю ЛАД складемо рівняння Максвела машини в диференційній формі, використовуючи кординатну систему
x, y, z статора

;

,

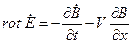де V – швидкість переміщення бігуна.

Як видно з моделі, наше поле одномірне:

; ; (19)

Ці ж рівняння в інтегральній фoрмі мають вигляд

, (20a)

. (20б)

В рівняннях (18), (20) позначено J_(1,2) – густина струмового шару машини (статора, ротора); L_H – контур інтегрування по ; S_H – площа, яку охоплює контур L_H; L_E – контур інтегрування по ; S_E – площа, яку охоплює контур L_E. Для одномірного поля, нехтуючи спадами напруженості в проводах, матимемо

;

,

або

,

.

З другого рівняння системи (21) визначимо і підставимо це значення у перше рівняння цієї ж системи, після чого отримуємо

. (22)

Розв’язок рівняння (22) шукаємо для усталеного режиму, як частковий розв’язок неоднорідного рівняння при відомій густині струму статора

(23)

у вигляді .

Підставляючи розв’язок (23) в (22) отримаємо

; . (24)

Точний розв’язок рівняння (22) ще має включати загальний розв’язок однорідного рівняння (22), для отримання якого у (22) використаємо підтановку

B(x,t)=X(x)×T(t). (25)

Використовуючи (25) у (22) без правої частини, розділивши змінні, отримаємо

, (26)

де l – стала величина

З рівняння

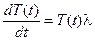(27)

визначаємо , де С – стала інтегрування

Подібно з рівняння

(28)

визначаємо

, (29)

де – корені характеристичного рівняння (28).

Стала l в загальному випадку може бути дійсною, уявною або комплексною величиною, але для нашого випадку, коли розглядаються усталені процеси і джерелом живлення є періодична НС статора з частотою , ми повинні прийняти .Враховуючи це можемо представити

і далі

(30)

де ; ; .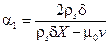

Тому кінцево рзвя’зок (22), враховуючи (24), (29) та (30) можемо записати у вигляді

. (31)

Усі складові рзв’язку (31) є періодичними функціями часу. Перша складова, судячи за її структурою, це основна вимушена прямобіжна хвиля поля, параметри якої визначаються співвідношеннями (23), (24). Другий доданок (31) це прямобіжна згасальна з коефіцієнтом хвиля поля, зумовлена розривом магнітопровода машини зі сторони входу основної хвилі. Третій доданок – це зворотньобіжна згасальна з коефіцієнтом хвиля поля, зумовлена розривом магнітопроводу машини зі сторони виходу основної хвилі. Два останні доданки, тобто обдві згасальні хвилі поля, зумовлені кінцевими ефектами мають однакову довжину півхвилі , яка відрізняється від довжини півхвилі основного поля t, та мають однакові швидкості переміщення

. (32)

Але глибина проникнення прямобіжної згасальної хвилі – більша від глибини проникнення зворотньозгасальної біжної згасальної хвилі і тому прямобіжна хвиля кінцевого ефекту може проникнути до кінця магнітопроводу машини та істотно змінити її результуюче поле ї характеристики. Зворотньобіжна хвиля кінцевого ефекту згасає швидко та існує тільки поблизу вихідного кінця. Вона не може істотно змінити результуюче поле машини і тому нею звичайно нетують. Отже, основна хвиля поля та згасальна прямобіжна хвиля кінцевого ефекту інтерферуючи між собою залежно від швидкості переміщення бігуна можуть або підсилювати або ослабляти одна одну і від цього буде залежати величина результуючого поля машини та її тягове зусилля.

Якщо прийняти, що густина струму J₁, яка визначається за (23), є сталою по довжині машини, то миттєве значення зусилля двигуна обчислюється

, (33)

де B(x) – визначають за (31), D – довжина пакету магнітопроводу, L– довжина індуктора.

Середнє значення тягового зусилля машини F_cp обчислюється за виразом

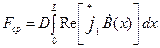, (34)

де – величина, спряжена з , яка визначається з (23)

На рис.7 показана залежність тягового зусилля для ЛАД з постійним значенням густини струму, коли не врахована згасальна прямобіжна хвиля кінцевого ефекту – крива 1 та врахована – крива 2. [Ямамура ЭА Изд. ЛО 1983].

Рис.7. Залежність зусилля при розмірі індуктора – 5000х5000мм²

До ЛАД за фізичними явищами дуже подібними є АД з дуговим статором., конструкційна схема якого наведена на рис.? Звичайно діаметр D феромагнітного барабана, який тут виконує роль ротора є задання і досягає значної величини, а його частота обертання повинна бути низькою.

Щоби забезпечити цю частоту кількість пар полюсів р машини повинна бути достатньо великою. Якщо для того отримати на валу барабана потрібний електромагнітний момент достатньо розташувати обмотку статора не на повній дузі 360°, а на дузі g_D (див. рис.8).

Рис.8. Конструкційна схема AD з дуговим статором

Тоді кутову синхронну частоту обертання поля двигуна з кількістю пар полюсів P_D – W_CD можна записати через лін.синхр.швидк

,

,

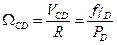де 2p_Dt=g_DR (див.рис.8); R=

Електромагнітний момент такої машини

,

де р – кількість пар полюсів машини, якщо би в машині була би обмотка статора по повній його дузі 360° з кількістю пар полюсів .

Дата добавления: 2015-10-24