
Читайте также:
|
Задача 5.1
 Приемник соединен звездой (рис. 5.1, а):
Приемник соединен звездой (рис. 5.1, а):
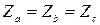 =80- j 60, линейное напряжение
=80- j 60, линейное напряжение
источника 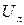 = 220 В.
= 220 В.
|
 Решение
Решение
Однофазная схема приведена на рис. 5.1, б.
|
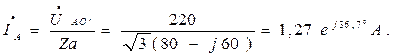
Ток в фазах В и С:
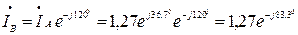 А,
А,
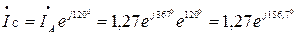 А.
А.
Активная мощность:
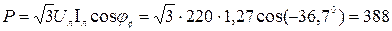 Вт.
Вт.
Реактивная мощность:
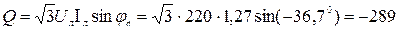 Вар.
Вар.
Полная мощность:
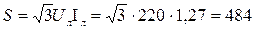 ВА.
ВА.
Векторная диаграмма приведена на рис. 5.1, в:
|

Задача 5.2
 Приемник соединен звездой (рис. 5.2):
Приемник соединен звездой (рис. 5.2):
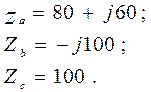
Фазное напряжение источника 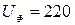 В.
В.
Рассчитать токи при наличии и отсутствии
нулевого провода.
|
Решение
Обозначим:
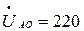 В;
В; 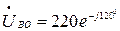 В;
В; 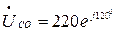 В.
В.
1. При наличии нулевого провода:
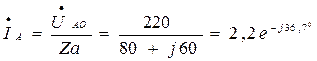 А,
А,
 А,
А,
 А,
А,
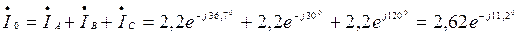 А.
А.
2. Без нулевого провода:


Фаза напряжения приемника:
 В,
В,
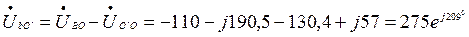 В,
В,
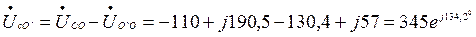 В.
В.
Линейные токи:
 А,
А,
 А,
А,
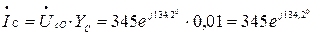 А.
А.
Задача 5.3
|
 Для определения следования фаз трехфазной системы напряженийприменяется прибор, состоящий из двух одинаковых ламп накаливаниясопротивлением R и конденсатором емкостью С, соединенных звездой (рис. 5.3). При частоте f = 50 Гц реактивная проводимость конденсатора wC равна активной проводимости лампы wC = 1/R
Для определения следования фаз трехфазной системы напряженийприменяется прибор, состоящий из двух одинаковых ламп накаливаниясопротивлением R и конденсатором емкостью С, соединенных звездой (рис. 5.3). При частоте f = 50 Гц реактивная проводимость конденсатора wC равна активной проводимости лампы wC = 1/R Система линейных напряжений симметрична:  В.
В.
Определить напряжение на лампах при прямом и обратном порядке следования фаз.
Решение
1. При прямом порядке следования фаз
 В,
В,  В,
В,  В.
В.
Напряжение смещение нейтрали:
 где
где 
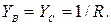
Напряжение на лампах
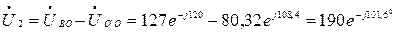 В,
В,
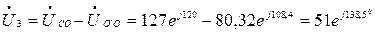 В.
В.
2. При обратном порядке следования фаз
 В,
В,  В,
В, 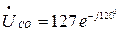 В.
В.
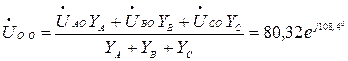
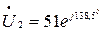 В,
В, 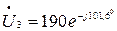 В.
В.
Таким образом, ярче горит лампа, включенная в фазе, напряжение которой отстает от напряжения фазы А.
Задача 5.4
 Приемник соединен треугольником (рис. 5.4, а)
Приемник соединен треугольником (рис. 5.4, а) 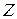 = 16 + j 12 Ом, линейное напряжение источника
= 16 + j 12 Ом, линейное напряжение источника 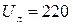 В. Определить линейные и фазные точки, построить векторную диаграмму.
В. Определить линейные и фазные точки, построить векторную диаграмму.
Решение
Примем что комплекс напряжения 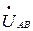 - действителен
- действителен 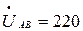 В, тогда
В, тогда  В,
В, 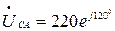 В.
В.
|
|
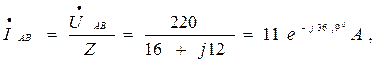

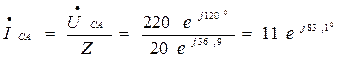 А,
А,
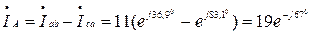 А,
А,

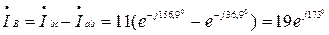 А,
А,
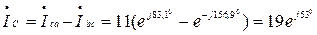 А. Векторная диаграмма приведена на рис. 5.4, б.
А. Векторная диаграмма приведена на рис. 5.4, б.
|
Задача 5.5
 Приемник соединен треугольником
Приемник соединен треугольником
(рис. 5.5). Сопротивление фаз приемника  =10
=10 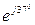 , сопротивление линейных проводов
, сопротивление линейных проводов 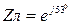 Ом,
Ом,  В.
В.
Определить линейные и фазные токи напряжения приемника.
Рис. 5.5
Решение
Преобразуем треугольник в звезду:
 Ом.
Ом.
Примем: 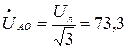 В,
В, 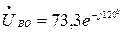 В,
В,  В.
В.
Определяем линейные токи:
 А,
А,
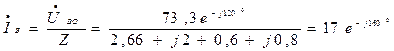 А,
А,
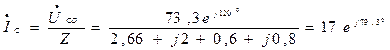 А.
А.
Определяем напряжение приемника:
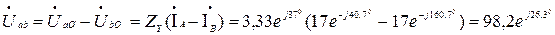 В,
В,
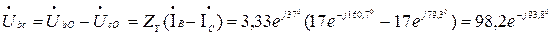 В,
В,
 В,
В,
Фазные токи треугольника:
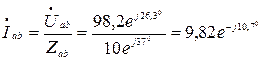 А,
А,
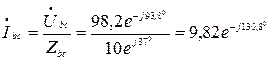 А,
А,
 А.
А.
Задача 5.6
 Группы ламп включены в трех фазную
Группы ламп включены в трех фазную
сеть, как показано на рисунке. В каждой группе лампы соединены параллельно, причем 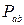 = 440 Вт,
= 440 Вт, 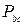 = 1100 Вт,
= 1100 Вт,  = = 2200 Вт. Линейное напряжение источника
= = 2200 Вт. Линейное напряжение источника 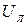 =220 В.
=220 В.
Определить фазные и линейные токи.
|
Решение
Принимаем:

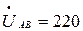 В,
В,  В,
В, 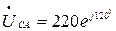 В.
В.
Определяем фазные и линейные токи:
 А,
А,
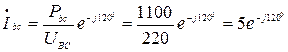 А,
А,
 А.
А.
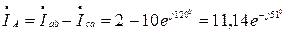 А,
А,
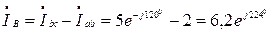 А,
А,
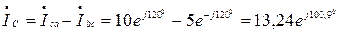 А.
А.
Задача 5.7
 Три одинаковых сопротивления
Три одинаковых сопротивления 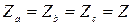 соединены звездой и подключены к трехфазной сети с линейным напряжением
соединены звездой и подключены к трехфазной сети с линейным напряжением  В (рис. 5.7, а). Определить показание вольтметра.
В (рис. 5.7, а). Определить показание вольтметра.
|
Решение
 Идеальный вольтметр имеет бесконечно большое сопротивление, следовательно такое включение аналогично разрыву линейного провода, а показание вольтметра равно напряжению между точками А и а на векторной диаграмме (рис. 5.7, б).
Идеальный вольтметр имеет бесконечно большое сопротивление, следовательно такое включение аналогично разрыву линейного провода, а показание вольтметра равно напряжению между точками А и а на векторной диаграмме (рис. 5.7, б).
Из треугольника Aba:
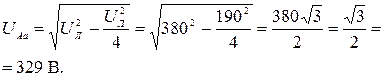
|
Задача 5.8
 Определить показания амперметра в цепи, приведенной на рис. 5.8, если
Определить показания амперметра в цепи, приведенной на рис. 5.8, если 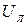 = = 380 B,
= = 380 B,  = 10 Ом,
= 10 Ом, 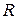 = 80 Ом.
= 80 Ом.
Решение
Представим фазные напряжения источника в виде: 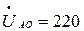 В,
В,
 В,
В,
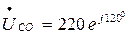 В.
В.

Напряжения между точкой b (или с) и нулем генератора:
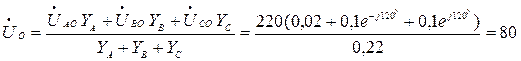 В,
В,
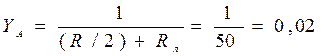 Ом,
Ом,
 Ом.
Ом.
Тогда 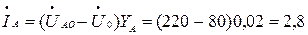 А,
А,
Следовательно:
 А,
А,
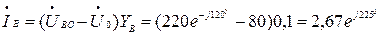 А,
А,
 А.
А.
Задача 5.9
Фазное напряжение симметричного источника 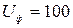 В, сопротивление в фазах приемника R = wL = 1/(wC) =10 Ом. Определить показания ваттметра (рис. 5.9), потребляемую в цепи активную мощность.
В, сопротивление в фазах приемника R = wL = 1/(wC) =10 Ом. Определить показания ваттметра (рис. 5.9), потребляемую в цепи активную мощность.

|

Решение
Принимаем:
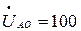 В,
В,
 В,
В,
 В.
В.
Определяем линейные точки:
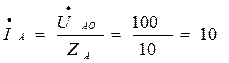 А,
А,
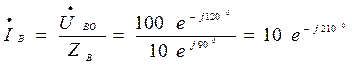 А,
А,
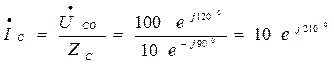 А.
А.
Ток в нейтральном проводе:
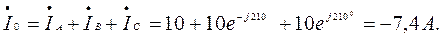
Напряжение на зажимах ваттметра:
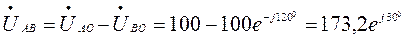 В.
В.
Показание ваттметра:
 Вт.
Вт.
Потребляемая активная мощность:
Р = 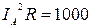 Вт.
Вт.
Задача 5.10
Три одинаковые нагрузки сопротивлением 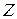 = 10+ j 10 Ом, соединены звездой (рис. 5.10) и подключены к трехфазной сети с напряжением
= 10+ j 10 Ом, соединены звездой (рис. 5.10) и подключены к трехфазной сети с напряжением 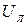 =380 В.
=380 В.
 Определить показания ваттметра и реактивную мощность цепи.
Определить показания ваттметра и реактивную мощность цепи.
|

Решение
Принимаем:
 В,
В,
 В,
В,
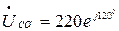 В.
В.
Напряжение на зажимах ваттметра:
 В.
В.
Ток, протекающий в обмотке прибора:
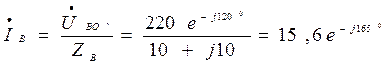 А.
А.
Показание ваттметра:
 Вт.
Вт.
Реактивная мощность:
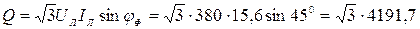 Вар.
Вар.
Таким образом, показание ваттметра при таком включении равно 
Задача 5.11

 К симметричному трехфазно-му генератору (рис. 5.11, а) с фазной э.д.с.
К симметричному трехфазно-му генератору (рис. 5.11, а) с фазной э.д.с. 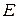 = 230 В и с внутреннем сопротивлением
= 230 В и с внутреннем сопротивлением 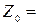 (0,3+j0,9) Ом подключена не симметричная нагрузка, соединенная в звезду с нулевым проводом. Сопротивление фаз нагрузки
(0,3+j0,9) Ом подключена не симметричная нагрузка, соединенная в звезду с нулевым проводом. Сопротивление фаз нагрузки 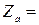 (2+ j 4) Ом,
(2+ j 4) Ом, 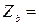 (4 - j 8) Ом,
(4 - j 8) Ом,  5 Ом.
5 Ом.
Сопротивление каждого провода линии 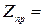 (0,4+ j 0,3) Ом, а сопротивление нейтрального провода
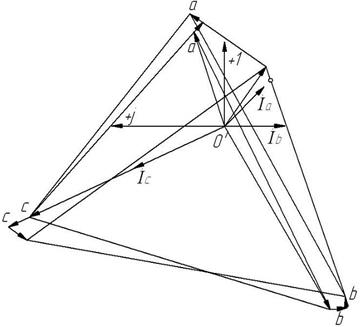
(0,4+ j 0,3) Ом, а сопротивление нейтрального провода  5 Ом. Определить токи и направления на каждой фазе нагрузки и генераторе при наличии нейтрального провода и без него. Для каждого случая построить векторные диаграммы.
5 Ом. Определить токи и направления на каждой фазе нагрузки и генераторе при наличии нейтрального провода и без него. Для каждого случая построить векторные диаграммы.
Решение
Запишем фазные э.д.с. генератора в комплексном виде:
 В,
В, 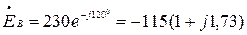 В,
В,
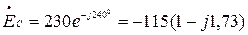 В.
В.
Комплексные проводимости фаз:
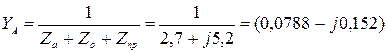 Ом-1,
Ом-1,
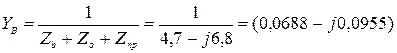 Ом-1,
Ом-1,
 Ом-1.
Ом-1.
Найдем напряжение между точками 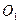 и
и 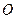 по формуле:
по формуле:

При наличии нейтрального провода:

Определим токи:
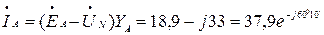 А,
А,
 А,
А,
 А,
А,
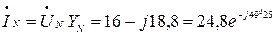 А.
А.
Проверка показывает, что:
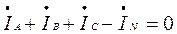
Напряжение на фазах нагрузки:
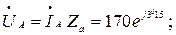
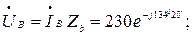
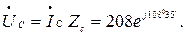
Напряжение на каждой фазе генератора:
 В,
В,
 В,
В,
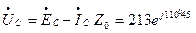 В.
В.
|
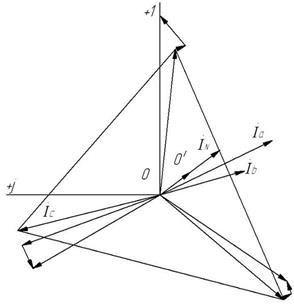
При обрыве нейтрального провода:
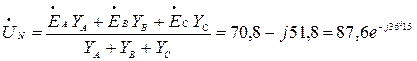 В.
В.
Токи:
 А,
А,
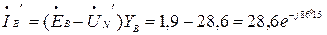 А,
А,
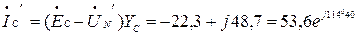 А.
А.
Напряжение на фазах нагрузки:


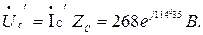
Напряжение на фазах генератора:
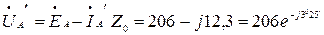 В,
В,
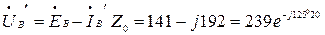 В,
В,
 В.
В.
|
 Задача 5.12
Задача 5.12
Дано: рис. 5.12 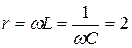 Ом,
Ом, 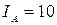 А.
А.
Найти:
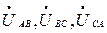
|
Решение
При соединении нагрузки в 
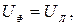 тогда:
тогда:
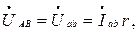
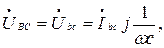


Для нахождения токов 
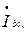
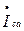 воспользуемся законами Кирхгофа:
воспользуемся законами Кирхгофа:
 (для узла a),
(для узла a),
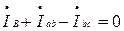 (для узла в),
(для узла в),
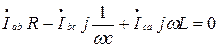 (для контура abc).
(для контура abc).
Подставим в третье уравнение численные значения и преобразуем к виду:

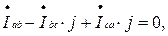
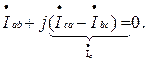
Для узла с именем: 
Откуда: 
Тогда система примет вид:
 ,
, 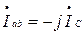 ,
, 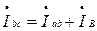 .
.
где:
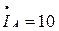 А,
А, 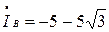 А,
А, 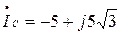 А.
А.
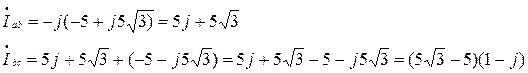

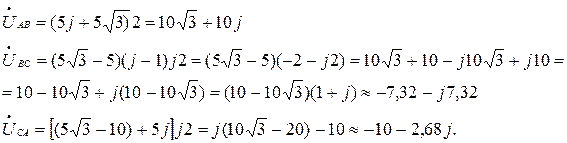
Проверка:
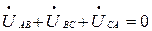
Задача 5.13
 Дано: рис. 5.13, а
Дано: рис. 5.13, а
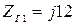 Ом,
Ом,
 Ом,
Ом,
 Ом,
Ом,
 В.
В.
Определить показания приборов.

Решение
Применим метод симметричных составляющих. Схема замещения имеет вид (рис. 5.13, б):
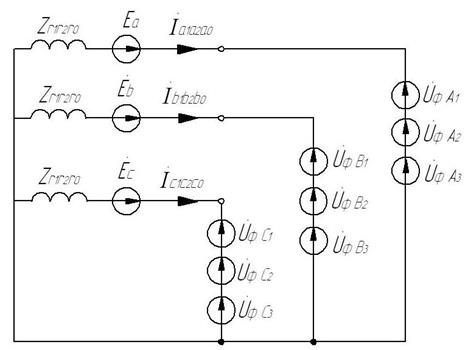
Рис. 5.13, б
Проведем расчет для фазы А:

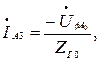
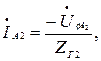

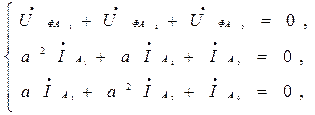

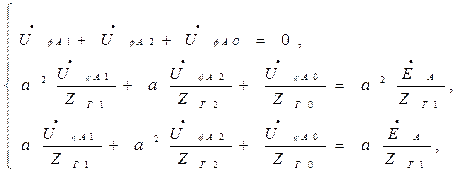
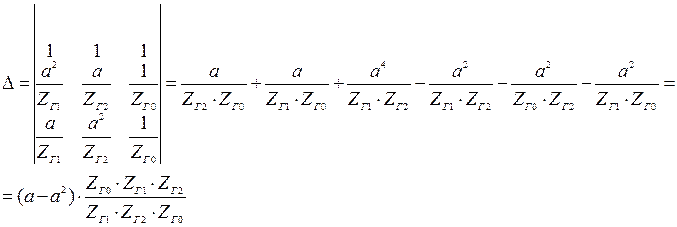
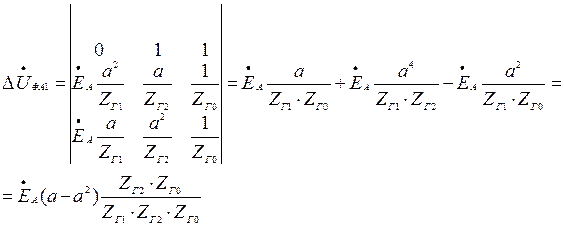

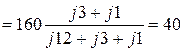 В.
В.
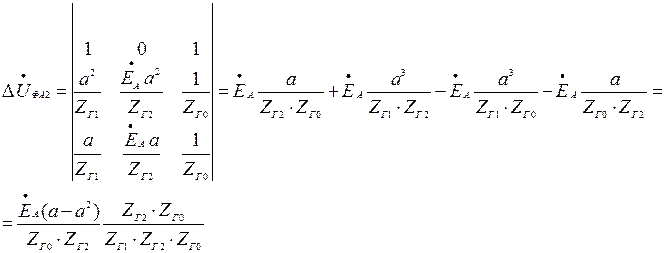

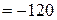 В.
В.
 находим из
находим из  :
:
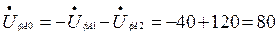 В.
В.
 = 30
= 30 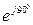 А.
А.
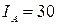 А.
А.
Для нахождения показаний 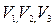 необходимо найти
необходимо найти  .
.
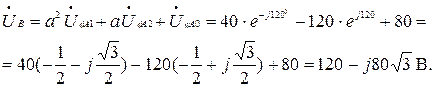
 В.
В.

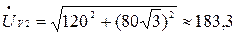 В.
В.
 В.
В.
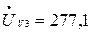 В.
В.
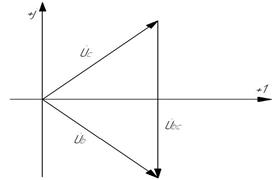
Построим векторную диаграмму для  (рис. 5.13, в).
(рис. 5.13, в).
|
Задача 5.14
 Три приемника сопротивления (рис. 5.14)
Три приемника сопротивления (рис. 5.14) 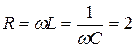 Ом, подключены к трехфазной цепи с фазным напряжением
Ом, подключены к трехфазной цепи с фазным напряжением 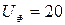 В.
В.
Определить фазные токи:
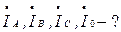
|
Решение
Так как нагрузка не симметрична 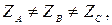 то по проводу протекает уравнительный ток
то по проводу протекает уравнительный ток 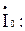
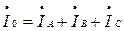 .
.
Нужно найти напряжение смещение нейтрали 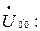
 ,
, 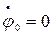 .
.
Применим метод узловых потенциалов:
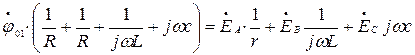
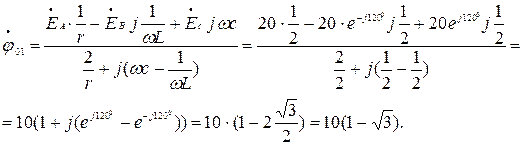
По второму закону Кирхгофа находим:
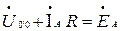
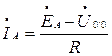


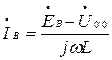

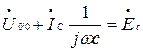
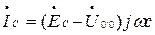

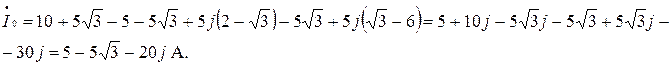
Задача 5.15
Приемник энергии, сопротивления фаз которого одинаковы, потребляют мощность 5,46 кВт при cos jф = 0,8 (jф >0). Линейное напряжение на нагрузке равно 370 В. Чему равна фазная ЭДС генератора, соединенного звездой, внутреннее сопротивление каждой фазы которого Z0 = (0,3 + j 0,9) Ом, а сопротивление каждого провода линии Zп р = (0,4 + j 0,8) Ом?
Ответ: Еф = 230 В.
Задача 5.16
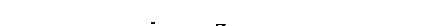
К симметричному трех-фазному генератору с фазной ЭДС E = 230 В и с внутренним сопротив-лением Z 0 = (0,3+ j 0,9) Ом подключена несимметрич-ная нагрузка, соединенная в звезду с нулевым проводом. Сопротивление фаз нагрузки: Z a= (2+ j 4) Ом; Z b= (4- j 8) Ом; Z C = 5 Ом. Сопротивление каждого повода линии Z пр= = (0,4+ j 0,8) Ом, а сопротивление нулевого провода Z N = 0,5 Ом.
Определить токи и напряжения на каждом фазе нагрузки и генератора при наличии нулевого провода и при его обрыве.
Ответ: 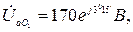
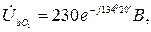
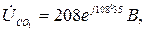
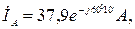
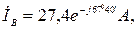
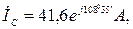
 при обрыве:
при обрыве: 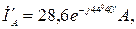


Задача 5.17
Линейные напряжения трехфазной сети: U AB = 120 В, U BC = 125 В. К этой сети подключена нагрузка, соединенная треугольником, сопротивление фаз которой Z AB = 25 Ом, Z BC = 20 Ом, Z CA = 20 Ом. Найти линейные и фазные токи.
Ответ: I AB = 4,8 А, I BC = 5,5 А, I CA = 6,98 А, I A = 9,15 А, I B = 8,68 А, I C = 11,9 А.
Дата добавления: 2015-10-24; просмотров: 456 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Цепи со взаимной индуктивностью. | | | Harry Potter and the Sorcerer's Stone |