Резонансные явления.

Задача 3.1

В цепи , R = 10 Ом, L = 100 мкГн, С = 100 пФ (рис. 3.1).

Определить: 1) резонансную частоту; 2) резонансный ток; 3) напряжение U_L и U_C при резонансе; 4) характеристическое сопротивление; 5) затухание и добротность контура; 6) значение энергий магнитного и электрического полей при резонансной частоте.

Рис. 3.1

Решение

1. Резонансная частота:

1/сек, f ₀ = =1,59·10⁶ Гц.

2. Резонансный ток: I ₀ = = 5 A.

3. Напряжение на зажимах индуктивного и емкостного сопротивлений при резонансе:

U _L0= U _C0 = LI ₀ = 10⁷ · 100 · 10^-6 · 5 = 5 · 10³ В.

4. Характеристическое (волновое) сопротивление: Ом.

5. Затухание и добротность контура:

, .

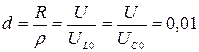6. W_{Cma x} = W _{L ma x} = = C =100 · 10^-6 · 5²= 25 · 10^-4 Дж.

Задача 3.2

Дана цепь u = 10sin 10² t, R = 10Ом, L= 0,4мГн, С₁ = 0, 1 мкФ. Цепь находится в состоянии резонанса (рис. 3.2).

Определить: 1) С₂; 2) I₁, I₂, I; 3) мощность.

Решение

Определение резонанса для параллельного контура:

Im Y = Im(g + jb) = b = 0.

Проводимость левой ветви ,

проводимость правой ветви Y ₂ = (C₁+C₂) потребляемую цепью.

Рис. 3.2

Тогда проводимость цепи:

Y=Y₁+Y₂

Следовательно, ,

откуда С ₂ = = 0,135 мкФ.

Токи в ветвях: = 0,172 А,

=0,166 А,

0,25 · 10^-1 мА.

Мощность, потребляемая цепью:

0,172² · 10=0,3 Вт.

Задача 3.3

В цепи U = 50 В, R = 25 Ом, L’ = 2 мГн, L = 0,4 мГн, С = 1 мкФ.

Определить: 1) резонансные частоты; 2) для каждой резонансной частоты токи в ветвях и токи в неразветвленной части цепи.

Для каждой резонансной частоты показать (в общем виде), что максимальные значения энергий магнитного и электрического полей равны между собой (рис. 3.3).

Рис. 3.3

Решение

1) Резонансная частота параллельного контура LC:

, .

Резонансная частота цепи как последовательного контура определится из уравнения:

Im Z (ω)=0,

.

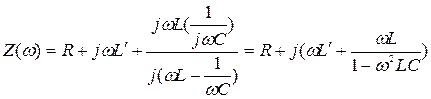Следовательно , отсюда .

Таким образом 1/сек,

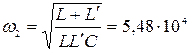1/сек.

2) При частоте ω₁ параллельный контур без потерь настроен в резонанс (резонанс токов), следовательно, сопротивление параллельного контура равняется бесконечности и поэтому ток в неразветвленной части цепи I = 0 напряжение на параллельном контуре U_LC = U, поэтому:

2,5 А.

При частоте ω₂ цепь находится в состоянии резонанса напряжений и, следовательно:

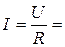2 А,

а напряжение на индуктивности равно напряжению на параллельном участке цепи LC:

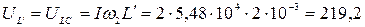В,

тогда

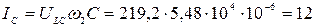А,

А.

При частоте ω₁ ток в неразветвленной части равняется нулю и поэтому максимальное значения энергий магнитного и электрического полей определяются выражениями:

, ,

.

Однако, 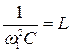, а I_C = I_L, поэтому:

,

При частоте ω₂:

, ,

.

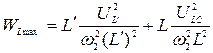Так как , то

.

Задача 3.4

Цепь находится в состоянии резонанса; U = 5 В, С = 40 мкФ, L = 100 мГн, W_{Cma x} = 10^-1 Дж (рис. 3.4).

Определить: Q, I ₀.

Рис. 3.4

Задача 3.5

Параллельный контур в цепи настроен в резонанс при частоте w = 5·10⁴ 1/сек, С = 0,4 мкФ, I₁ =2 А (рис. 3.5).

Определить: напряжение на активном сопротивлении.

Задача 3.6

Цепь находится в состоянии резонанса, U = 30 В, ω = 5·10³ 1/сек,

I = 225 мА, I₁ = 375 мА (рис. 3.6).

Определить:емкость конденсатора.

Задача 3.7

Цепь (рис. 3.7) находится в состоянии резонанса I ₁ = 7 A,

I = 3,6 A.

Определить: I₂.

Рис. 3.7

Задача 3.9

Определить емкость конденсатора последовательного контура, частота собственных колебаний которого f₀ = 300 кГц, а индуктивность L = 2 мГн.

1. 140 пФ.	2. 300 пФ.	3. 0,005 мкФ.
4. 1200 пФ.	5. 0,1 мкФ.
Ответ: 1

Задача 3.10

Напряжения на реактивных элементах последовательного колебательного контура при резонансе равны 250 В, напряжение питания равно 5 В.

Определить активное сопротивление r контура, если его характеристическое сопротивление равно 100 Ом.

1. r = 20 кОм.	2. r = 2 кОм.	3. r = 200 Ом.
4. r = 20 Ом.	5. r = 2 Ом.
Ответ: 5

Задача 3.11

Индуктивность последовательного колебательного контура L = 25 мкГн, активное сопротивление r = 10 Ом, емкость C = 15,8 пФ.

Определить напряжение на емкости при резонансе, если напряжение на контуре 1 В.

1. 12,56 мВ.	2. 125,6 мВ.	3. 1,256 В.
4. 12,56 В.	5. 125,6 В.
Ответ: 5

Задача 3.12

В цепи имеет место резонанс токов.

Определить резонансную частоту w₀ если параметры цепи: C = 200 пФ, L = = 1 мГн, r = 2 кОм.

Рис. 3.12

1. 10^6 рад/с	2. 10^8 рад/с	3. 2,24∙10^6 рад/с
4. 3∙10^6 рад/с	5. 10^5 рад/с
Ответ: 1

Глава 4.

Дата добавления: 2015-10-24