
Читайте также:
|
Глава 1.
Линейные электрические цепи постоянного тока.
Задача 1.1
На рис. 1.1 показана схема электрической цепи с резисторами, сопротивления которых R1 = 18 Ом, R2 = 30 Ом, R3 = 20 Ом. Определить токи ветвей, если напряжение U = 120 В.
Решение
 Решение проводим методом свертывания. Эквивалентное сопротив-ление разветвленного участка цепи:
Решение проводим методом свертывания. Эквивалентное сопротив-ление разветвленного участка цепи:


Общее сопротивление цепи:

В соответствии с законом Ома ток:

Напряжение на зажимах параллельных ветвей:

Или на основании второго закона Кирхгофа:

Токи ветвей:




Задача 1.2
Пользуясь принципом взаимности, определить ток I3 в схеме цепи рис. 1.2, а, если источник ЭДС E3 будет включен в ветвь с резистивным элементом R5 (рис.1.2, б). E3 = 48 В, R2 = 16 Ом, R3 = 8 Ом, R4 = 16 Ом, R5 = 8 Ом.

а) б)
Рис. 1.2
Решение
Определяем эквивалентное сопротивление RЭК цепи:

Тогда



Задача 1.3

Найти напряжение U4 на сопротивлении R4 (рис. 1.3), если известно, что Е = 60 В, Rвн = R1 = = 2Ом, R2 = 4 Ом, R3 = 1 Ом, R4 = = 3 Ом.
Рис. 1.3
Решение
Эквивалентное сопротивление последовательно соединенных сопротивлений R3 и R4:
R34 = R3 + R4 = 1+3 = 4 Ом.
Эквивалентное сопротивление параллельно соединенных сопротивлений R2 и R34 найдем из соотношения 1/ R12 = 1/ R2 +1/ R34, откуда
R12 = R2 R34 / R2 + R34 = 4∙4 / 4+4 = 2 Ом.
По закону Ома для замкнутой цепи найдем силу тока в неразветвлённой части цепи:
I = Е/(Rвн + R1 + R12) = 60/(2 + 2 + 2) = 10 А.
При этом падение напряжения между узлами 1 и 2 U12 = I · R12 = 10·2 = 20 В.
Сила тока в ветви с сопротивлениями R3 и R4
I34 = Ul2 / (R3 + R4) = 20/(1 + 3) = 5 А,
а падение напряжения на сопротивлении R4: U4 = I34 ∙ R4 = 5∙3= 15 В.
Задача 1.4
В схеме цепи рис. 1.4 определить напряжение UAB, если R1 = 30, R2 = 5 Ом,
R3 = 20 Ом, R4 = 10 Ом. Значение ЭДС E = 45 В.
Решение
 Для определения UAB нужно найти токи I и I1. Применяя метод свертывания, найдем RЭК DB. Очевидно, резистивные элементы с сопротивлениями 5 и 10 Ом соединены последовательно, а с сопротивлением 30 Ом - параллельно:
Для определения UAB нужно найти токи I и I1. Применяя метод свертывания, найдем RЭК DB. Очевидно, резистивные элементы с сопротивлениями 5 и 10 Ом соединены последовательно, а с сопротивлением 30 Ом - параллельно:


Тогда I = 45/30 = 1,5 А. Так как соотношение сопротивлений двух параллельных ветвей с сопротивле-ниями 30 и 15 Ом 2: 1, то ток I1 = = 1 А и будет вдвое больше тока I2. Зная токи I1 и I, обходим контур ABCA (мысленно замыкая его) и составляем уравнение по второму закону Кирхгофа:


Задача 1.5
В электрической цепи, схема которой приведена на рис. 1.5, а, известны ЭДС E = 30 В и все сопротивления R12 = 8 Ом, R23 = 12 Ом, R31 = 12 Ом, R4 = 5,5 Ом, R5 =7 Ом, R6 = 2 Ом. Определить силу тока в ветви с источником ЭДС.

а) б)
Рис. 1.5
Решение
Заменив треугольник сопротивлений 123 звездой сопротивлений (рис. 1.5, б), найдем сопротивления звезды:
R1 = R12R31 /(R12 + R23 + R31) = 8·12 / (8 +12 +12) = 3 Ом;
R2 = R12R23 / (R12 + R23 + R31) = 8·12 / (8 +12 +12) = 3 Ом;
R3 = R23R31 /(R12 + R23 + R31) = 12·12 / (8 +12 +12) = 4,5 Ом.
Сопротивление между точками 1 и 4:
R14 = R1 +  Ом.
Ом.
Сила тока в ветви с источником ЭДС Е:
I = E / (R6 + R14) = 30 / (2 + 8) = 3 А.
Задача 1.6
В электрической цепи, изображенной на рис. 1.6, а, E1 = 6 В, E2 = 3 В, R1 = R2 = = R3 = 10 Ом. Найти силу тока в ветви с сопротивлением R3.
Рeшение
Перейдя от источников ЭДС к источникам тока, получим

а) б)
Рис. 1.6
эквивалентную схему, изображенную на рис. 1.6, б, где
Ј1 = E1 / R1 = 6 / 10 = 0,6 А; g1 = 1 / R1 = 1 / 10 = 0,1 См;
Ј2 = E2 / R2 = 3 / 10 = 0,3 А; g1 = 1 / R2 = 1 / 10 = 0,1 См.
Источники тока образуют один эквивалентный источник тока (рис. 1.6, в),

в) г)
Рис. 1.6
где Јэкв’ = Ј1 + Ј2 = 0,6 + 0,3 = 0,9 А; gэкв = g1 + g2 = 0,1 + 0,1 = 0,2 См.
Перейдя от источника тока (рис. 1.6, в) к источнику ЭДС, получим схему цепи (рис. 1.6, г), эквивалентную исходной, где Eэкв = Јэкв / gэкв = 0,9 / 0,2 = 4,5 В,
Rэкв = 1 / gэкв = 1 / 0,2 = 5 Ом.
Искомая сила тока: I = Eэкв / (Rэкв + R3) = 4,5 / (5 + 10) = 0,3 А.
Задача 1.7
В электрической цепи (рис. 1.7) E1 = 50 В, E2 = 10 В, Ri1 = 0,4 Ом, Ri2 = 1 Ом, R1 = 3 Ом, R2 = R3 = 2 Ом. Требуется определить токи в ветвях.
Решение

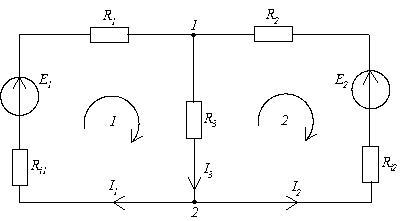 В схеме два узла и три ветви. Следовательно, по первому закону Кирхгофа необходимо составить одно уравнение, а по второму – два. Обозначим на схеме электрической цепи узлы, токи в ветвях и стрелками произвольно укажем их положительные направ-ления. Выберем два незави-симых контура и стрелками покажем направления их обхода. Составим уравнение по первому закону Кирхгофа для первого узла:
В схеме два узла и три ветви. Следовательно, по первому закону Кирхгофа необходимо составить одно уравнение, а по второму – два. Обозначим на схеме электрической цепи узлы, токи в ветвях и стрелками произвольно укажем их положительные направ-ления. Выберем два незави-симых контура и стрелками покажем направления их обхода. Составим уравнение по первому закону Кирхгофа для первого узла:
I1 + I2 – I3 = 0.
Составим уравнения по второму закону Кирхгофа для выбранных независимых контуров:
(R1 + Ri1)· I1 + R3 · I3 = E1 ,
– (R2 + Ri2)· I2 – R3 · I3 = – E2 .
Полученные уравнения образуют систему независимых уравнений с тремя неизвестными:
I1 + I2 – I3 = 0,
3,4 I1 +2 I3 = 50,
–3 I2 – 2 I3 = –10.
Решив эту систему, будем иметь: I1 = 10 А, I2 = – 2 А, I3 = 8 А. По полученным знакам токов устанавливаем, что действительные направления токов I1 и I3 совпадают, а тока I2 – противоположно произвольно выбранным положительным направлениям.
Проверку правильности расчета токов осуществляют по балансу мощностей.
Задача 1.8
Найти ток в ветви с источником ЭДС E2 в электрической цепи, схема которой приведена на рис. 1.8, а, если параметры цепи такие же как в примере 1.7.

Рис. 1.8, а
Решение
Приняв E2 = 0, получим схему, показанную на рис. 1.8, б.

Рис. 1.8, б
Для определения частичного тока 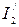 , созданного в ветви источником ЭДС E1 найдем вначале напряжение между узлами 1 и 2:
, созданного в ветви источником ЭДС E1 найдем вначале напряжение между узлами 1 и 2:
 В.
В.
Частичный ток
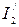 =
=  А.
А.
Ток 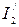 направлен от узла 1 к узлу 2.
направлен от узла 1 к узлу 2.
Приняв E1 = 0, получим схему, приведенную на рис. 1.8, в.

Рис. 1.8, в
Частичный ток  в рассматриваемой ветви найдем по закону Ома:
в рассматриваемой ветви найдем по закону Ома:
 =
=  А.
А.
Ток  направлен от узла 2 к узлу 1. Действительный ток в ветви I2 равен разности частичных токов I2 =
направлен от узла 2 к узлу 1. Действительный ток в ветви I2 равен разности частичных токов I2 = 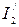 –
–  = 4,33 – 2,33 = 2 А. Он направлен от узла 1 к узлу 2.
= 4,33 – 2,33 = 2 А. Он направлен от узла 1 к узлу 2.
Задача 1.9
Найти токи в ветвях электрической цепи, схема которой приведена на рис. 1.9, если параметры ее такие же, как и в примере 1.7.
Рис. 1.9
Решение
Заземлим нижний узел, присвоив ему номер 0, а верхнему узлу - номер 1 (рис. 1.9). Система узловых уравнений в рассматриваемом примере состоит только из одного уравнения:
g11φ1 = J1.
Для определения узлового тока узла 1 целесообразно от источников ЭДС перейти к источникам тока:
J1' = E1 /(Ri1 + R1)= E1g1,
J2' = E1 /(Ri2 + R2)= E2g2.
Тогда
J1 = J1' + J2' = E1g1 + E2g2 = E l/(Ri1 + R1) + E2 /(Ri2 + R2) ≈ 18 А.
Определим собственную проводимость узла 1:
g11 = g1 + g2 + g3 = 1 /(Ri1 + R1) + 1/(Ri2 + R2) + 1/ R3 ≈ 1,13 См.
Подставив g11 и J1 в уравнение g11 φ1 = J1, найдем потенциал узла 1:
φ1 = J1 / g11 = 18/1,13 ≈ 16 В.
Определим токи в ветвях. Для этого запишем значение потенциала φ1, двигаясь от узла 0 к узлу 1 по ветви с источником ЭДС Е1:
φ1 = φ0 – Ri1I1 + El – R1I1, откуда с учетом того, что φ0 = 0, получим
I1 = (E1 - φ1)/(Ri1 + R1) = (50 - 16)/(0,4 + 3) = 10 A.
Для ветвей с сопротивлением R3 и источником ЭДС Е2 аналогично получим:
φ1 = φ0 + R3I3, откуда I3 = φ1 / R3 = 8 А, φ1 = φ0 + Ri2I2 + Е2 + R2I2. Тогда
I2 = (φ1 - E2)/(Ri2 + R) = (16 - 10)/(1 + 2)= 2 A.
Уравнение баланса мощностей:
E1I1 - Е2I2 = I12 (R1 + Ri1) + I22 (R2 + Ri2) + I32R3;
50∙10 – 10∙2=100∙(3 + 0,4) + 4∙(1+ 2) + 64∙2;
480 Вт = 480 Вт.
Задача решена правильно
Задача 1.10

В электрической цепи, схема которой приведена на рис. 1.10, дано: E1 = 6 В, E2 = 3 В, R1 = R2 = R3 = = 1 Ом. Требуется опреде-лить токи в ветвях.
Рис. 1.10
Решение
В схеме цепи два независимых контура. Произвольно обозначим на схеме положительные направления контурных токов I/ и I// стрелками, выбранные сопротивления контуров R11 = R1 + R3 = 1 + 1 = 2 Ом, R22 = R2+ R3 = 1 + 1= 2 Ом. Взаимные сопротивления R12 = R21 = – R3 = – 1 Ом. Контурные ЭДС E1 = E1 = 6 В, E11 = E2 = – 3 В.
Система контурных уравнений: R11 I/ + R12 I// = E1,
R21 I/ + R22 I// = E11,
Подставив найденные значения в систему контурных уравнений, получим:
2∙ I1 – I// = 6,
– I1 + 2∙ I// = –3.
Из первого уравнения системы: I// = 2 I1 – 6. Подставив I// во второе уравнение получим – I1 + 4 I1 – 12 = – 3, откуда I1 = 3 А, тогда I// = 2 I1 – 6 = 2·3 – 6 = 0.
Сила токов в ветвях: I1 = I/ = 3 А, I2 = I// = 0, I3 = I1 – I2 = 3 – 0 = 3 А.
Задача 1.11

Определить токи в ветвях электрической цени, изобра-жённой на рис. 1.11, методом контурных токов, если Е1 = = 50 В, Е2 = 75 В, J = 2 А, R1 = 30 Ом, R2 = 50 Ом.
Рис. 1.11
Решение
Независимые контуры и обход по ним выберем так, как показано стрелками на рис. 1.11. Тогда уравнение, связывающее контурные токи (I11 и I22) и ЭДС, имеет вид:
I11 ·(R1 + R2) + I22 · R12 = Е1 + Е2,
где I22 = J, R12=R2.
Из этого уравнения находим:
I1 = I11 =  А; I2 = I1 + J = 0,31 + 2 = 2,31 А.
А; I2 = I1 + J = 0,31 + 2 = 2,31 А.
Задача 1.12
Определить токи в ветвях электрической цепи (рис. 1.12) методом узловых потенциалов, если El = 20 В, E2 = 30 В, E3 = 2 В, E4 = 1,2 В, E5 = 5,6 В, R1 = = 50 Ом, R2 = 10 Ом, R3 = 20 Ом, R4 =10 Ом, R5 = 100 Ом, R6 = 50 Ом, R7 = = 20 Ом.
Решение
В тех случаях, когда в цепи имеется ветвь с идеальным источником ЭДС, целесообразно считать заземленным один из узлов именно этой ветви. Примем равным нулю потенциал узла 3, тогда потенциал узла 1 равен E1 = φ1 = 20 B.
Общее число требующихся для решения задачи уравнений уменьшается на одно, т. е. достаточно следующих уравнений:
g21 φ1 + g22 φ2 + g24 φ4 = JII; (12.1)
g41 φ1 + g42 φ2 + g44 φ4 = JIV.

Рис. 1.12
Определим собственные и взаимные проводимости узлов:
g22 = 1/ R3 + 1/ R4 + 1/ R6 = 1 / 10 + 1 /20 + 1 /50 = 0,17 См;
g44 = 1/ R4 +1/ R5 +1/ R7 = 1/20 + 1/10 + 1/20 = 0,2 См;
g12 = g21 = -1/ R6 = -1 /50 = -0,02 См;
g24 = g42 = -1/ R4 = -1 /20 = -0,05 См;
g14 = g41 = -1/ R7 = -1 /20 = -0,05 См.
Определим узловые токи:
JII = Е3 / Rз - E4 / R4 = 2/10 -1,2/20 = 0,14 А;
JIV = E4 / R4 + Е5 / R5 = 1,2/20 + 5,6/10 = 0,62 А.
Подставим полученные результаты в систему уравнений (12.1):
-0,02 ∙ 20 + 0,17 φ2 - 0,05 φ4 = 0,014; (12.2)
-0,05 ∙ 20 - 0,05 φ2 + 0,2 φ4 = 0,62.
Решив систему уравнений (12.2), определим потенциалы узлов 2 и 4:
φ2 = 6 В, φ4 = 9,6 В.
Пользуясь законом Ома, определим токи в ветвях:
I1 = 0,2 А; I2 = 0,2 А; I3 = 0,4 А; I4 = 0,12 А; I5 = 0,4 А; I6 = 0,28 А;
I7 = 0,52 А.
Ток в ветви с источником ЭДС Е1 определяется no первому закону Кирхгофа:
IЕ1 = I6 + I7 + I8 - I2 = 0,2 + 0,28 + 0,52 - 0,2 = 0,8 А
Или
IE1 = I6 + I3 + I5 - I2 = 0,2 + 0,4 + 0,4 - 0,2 = 0,8 А.
Уравнение баланса мощностей показывает, что мощность источников ЭДС примерно равна мощности нагрузки.
Задача 1.13


 В схеме электрической цепи, приведенной на рис. 1.13, найти ток I2, если звестно, что El = 10 В, Е2 = 2 В, R1 = R2 = R3 = 1 Ом.
В схеме электрической цепи, приведенной на рис. 1.13, найти ток I2, если звестно, что El = 10 В, Е2 = 2 В, R1 = R2 = R3 = 1 Ом.
Решение
Используем метод эквивалентного генератора. Разорвем ветвь электрической цепи в точках а, б и найдем напряжение между точками разрыва:
Еэкв = Uаб = Е1R3 /(R1 + R3) = 10 ∙ 1/(1+1) = 5 B.
Найдем сопротивление между точками разрыва:
Rэкв = Rаб = R1R3 /(Rl + R3) = 1 ∙ 1/(1 + 1) = 0,5 Ом.
Тогда I2 = (Uaб - Е2)/(Rаб + R2) = (Еэкв - Е2)/(Rэкв + R2) = (5 - 2)/(1 +0,5) = 2 A.
Задача 1.14
Определить ток I5 в измерительной диагонали неуравновешенного моста (рис. 1.14), воспользовавшись методом эквивалентного генератора, если E = 6 В, R1 = R2 = 1 кОм, R3 = 4 кОм, R4 = 2 кОм и R5 = 2,17 кОм.

Рис. 1.14
Решение
В соответствии с теоремой об эквивалентном генераторе воздействие всей цепи на рассматриваемую ветвь с резистором R5 можно заменить воздействием эквивалентного генератора (рис. 1.14, б), у которого:
Eэк = Uab хх; Rэк = Rab вх.
Для определения напряжения Uab хх разомкнем ветвь ab с резистором R5
(рис. 1.14, в):

Сопротивление Rab вх определяем по схеме рис. 1.14, г:

Ток диагонали находим из схемы рис. 1.14, д:

Ответ: I5 = 0,25 Ом.
Задача 1.15
В цепи (рис. 1.15) E = 20 В, J = 2 А, R = 15 Ом, R1 = 85 Ом. Определить токи, проверить баланс мощностей.
 Решение
Решение
Выберем положительное направление токов, составим уравнения по законам Кирхгофа. Цепь содержит три ветви (В = 3), два узла (У = 2), один источник тока (ИТ = 1). Число уравнений, составляемых по первому закону Кирхгофа:
У-1 = 1,
а по второму Закону Кирхгофа:
М = В-ИТ-У = 1.
Для узла а: I1 - J - I = 0.
Для контура, не содержащего источник тока:
IR + I1R1 = E,
Решая систему, получаем: I = -1,5 A, I1 = 0,5 A.
Составляем баланс мощностей: JUab + EI = I2R + I12R1,
предварительно определяя: JUab = I1R1 = 42,5 В.
Подставляя данные, имеем 42,5∙2+20∙(-1,5) = (-1,5)2∙15+0,52∙85 или 85 = 85. (Задачу можно решить и другим способом, применив преобразование источника тока в источник ЭДС).
Задача 1.16
 В цепи (рис. 1.16) определить сопротивление относительно зажимов 1-1’ в режиме холостого хода (зажимы 2-2’ разомкнуты) и короткого замыкания (зажимы 2-2’ соединены между собой). R1 = 160 Ом, R2 = 40 Ом, R3 = 40 Ом, R4 = 120 Ом.
В цепи (рис. 1.16) определить сопротивление относительно зажимов 1-1’ в режиме холостого хода (зажимы 2-2’ разомкнуты) и короткого замыкания (зажимы 2-2’ соединены между собой). R1 = 160 Ом, R2 = 40 Ом, R3 = 40 Ом, R4 = 120 Ом.
Ответ: 1. Режим холостого хода Rэ = 120 Ом.
2. В режиме короткого замыкания Rэ = 72 Ом.
Задача 1.17

 В цепи (рис. 1.17) R1 = 10 Ом, R2 = R3 = R5 = 25 Ом, R4 = 50 Ом, U = 120 В. Определитьтоки в ветвях цепи и показания вольтметра, включен-ного между точками с и d, считая, что его сопротивление во много раз превышает сопротивление каждого из элементов цепи. Показать, что если R2 / R4 = R3 / R5, то показания вольтметра V1 равно нулю.
В цепи (рис. 1.17) R1 = 10 Ом, R2 = R3 = R5 = 25 Ом, R4 = 50 Ом, U = 120 В. Определитьтоки в ветвях цепи и показания вольтметра, включен-ного между точками с и d, считая, что его сопротивление во много раз превышает сопротивление каждого из элементов цепи. Показать, что если R2 / R4 = R3 / R5, то показания вольтметра V1 равно нулю.
Ответ: Ucd = jc - jd = 0.
Задача 1.18
К зажимам двухполюсника, внутренняя схема которого неизвестна, подается постоянное напряжение, измеряемое вольтметром. При двух различных значениях этого напряжения измерены два соответствующих значения (см. табл.). Определить параметры генератора, эквивалентного двухполюснику.
| U,B | I,A |
Задача 1.19
Определить показания вольтметра (рис. 1.19), сопротивление которого велико по сравнению с R1 и R2.
|
|
|
|
|
|


|
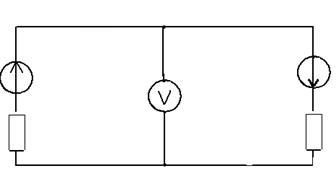
Ответ: 15 B.
Задача 1.20
В схеме моста (рис. 1.20) известны сопротивления резисторов R1 = 1300 Ом, R2 = 800 Ом, R3 = 400 Ом. Сопротивление гальванометра Rг = 600 Ом. Через сопротивление R1 протекает ток I 1 = 1 мА. К мосту приложено напряжение U = 2,5 В. Найти R4?
|

Ответ: 750 Ом.
Задача 1.21
 Методом узловых напряжений рассчитать токи в цепи (рис. 1.21).
Методом узловых напряжений рассчитать токи в цепи (рис. 1.21).
Указание. Если потенциал точки 4, являющейся общей для ЭДС E1 и E2, принять равным нулю (V4=0), то V3=-= E1, V4 = -E2 и для решения задачи достаточно составить всего одно уравнение узловой точки 1.
Ответ: I1 = 2,25 мА, I2 =1,4 мА, I3 = = 0,85 мА, I4 =0,75 мА, I5 =0,1 мА, I6 = 1,5 мА.
Задача 1.22
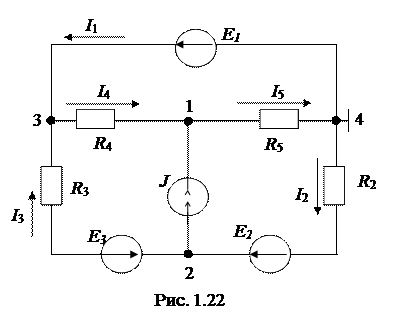 Дано: цепь (рис. 1.22) E1 = = 100 В, E2 = 150 В, E3 = 28 В, J = = 2 мА, R2 = 2 кОм, R3 = 4 кОм, R4 = 6 кОм, R5 = 8 кОм. Простейшим способом рассчитать токи всех ветвей.
Дано: цепь (рис. 1.22) E1 = = 100 В, E2 = 150 В, E3 = 28 В, J = = 2 мА, R2 = 2 кОм, R3 = 4 кОм, R4 = 6 кОм, R5 = 8 кОм. Простейшим способом рассчитать токи всех ветвей.
Ответ: I1 =3 мА, I2 =5 мА, I3 =3 мА, I4 =6 мА, I5 =8 мА.
Глава 2.
Электрические цепи однофазного синусоидального тока.
Задача 2.1
По известному комплексному току İ = (6 + j 8) А записать выражение для его мгновенного значения.
Решение
Находим: I =  = 10 А; Im = I
= 10 А; Im = I  = 14,1 А; ψ = arctg(8/6) = 53°7', следовательно, i (t) =14,1 sin(ω t + 53°7') А.
= 14,1 А; ψ = arctg(8/6) = 53°7', следовательно, i (t) =14,1 sin(ω t + 53°7') А.
Задача 2.2
Найти комплексную амплитуду и комплекс действующего значения тока, если его мгновенное значение описывается выражением i (t) = 14,1 sin(ω t + 30°) А.
Решение
Находим: İm = 14,1e j30° А, I = Im /  = 10 А, İ = 10е j30° А.
= 10 А, İ = 10е j30° А.
Задача 2.3
В сеть напряжением U = 220 В и частотой f = 50 Гц включается поочередно реостат с сопротивлением 10 Ом, индуктивная катушка с индуктивностью L = = 32 мГн и конденсатор емкостью 317 мкФ. Определить для каждого случая токи в приемниках, построить векторные диаграммы.

Рис. 2.3
Решение
Схемы замещения цепей представлены на рис. 2.3, а, б, в.
Комплексные сопротивления


Направление вектора 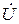 на комплексной плоскости выбираем по оси +1, тогда
на комплексной плоскости выбираем по оси +1, тогда 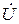 = 220ej° = 220 В.
= 220ej° = 220 В.
Комплексные действующие значения токов:



Мгновенные значения токов:



Векторные диаграммы построены на рис. 2.3, г, д, е.
Задача 2.4
Напряжение и ток пассивного двухполюсника равны 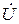 = (20 + j40) В,
= (20 + j40) В,
İ = (5 + j3) А. Построить векторную диаграмму на комплексной плоскости. Найти мгновенное напряжение и ток.
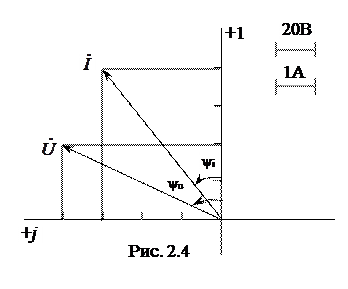
Решение
На комплексной плоскости с ортами +1 и + j строим векторы комплексных тока İ и напряжения 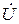 (рис. 2.4). Длины векторов пропорциональны в выбранном масштабе модулям комплексных действующих значений напряже-ния и тока:
(рис. 2.4). Длины векторов пропорциональны в выбранном масштабе модулям комплексных действующих значений напряже-ния и тока:


Их начальные фазы:


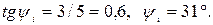
Комплексные действующие напряжение и ток в показательной форме:


Комплексные амплитуды напряжения и тока:

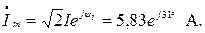
Мгновенные напряжения и ток:


Задача 2.5
В сеть напряжением 220 В включены последовательно катушка с активным сопротивлением 10 Ом и индуктивностью 159 мГн, а так же батарея конденсаторов. Определить емкость батареи, при которой в цепи установится резонанс напряжений. Найти ток в цепи и напряжение на индуктивном и емкостном элементах. Построить топографическую диаграмму напряжений.
 Решение
Решение
Схема замещения цепи представлена на рис. 2.5, а. Сопротивление ее реактив-ных элементов при резонансе равны: Lω = 1/(Cрез ω). Отсюда
Cрез = 1/(Lω 2) = 63,5 мкФ и XL = XC = 50 Ом.
 Комплексное входное сопротивление схемы при резонансе будет чисто активным
Комплексное входное сопротивление схемы при резонансе будет чисто активным  Ток
Ток 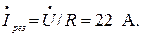
Напряжение на индуктивном и емкостных элементах равны между собой и значительно превышают входное напряжение: 
Поэтому внезапное установление резонанса напряжений в цепях может вызвать аварийную ситуацию, привести к пробою изоляции и т.д. Топографическая диаграмма напряжений при резонансе приведена на рис. 2.5, б.
Задача 2.6
Определить силу тока, падения напряжений на элементах и построить векторную диаграмму для цепи, схема которой показана на рис. 2.6, а, если известно, что U =120 В, ψu= 0, R = 6 Ом, L = 25,5 мГн, f = 50 Гц.
Решение
Находим:
xL = ωL =2π f L =2∙3,14∙50∙25,5∙10 -3 = 8 Ом;
Z = R + jxL = 6 + j 8 = 10е j 53° Oм;
İ = Ù / Z = 120/(10е j 53°) = 12e - j 53° А;
ÙR = R İ = 6∙12e - j 53° = 72е - j 53° В;
ÙL = jхL İ = 8∙12е - j 53° е j 90° = 96e j 37° В.
Векторная диаграмма приведена на рис. 2.6, б. Ток в рассматриваемой цепи отстает по фазе от приложенного к ней напряжения на угол φ = 53°.
|

а) б)
Рис. 2.6
Задача 2.7
Определить силу тока, падения напряжений на элементах и построить векторную диаграмму для цепи, схема которой показана на рис. 2.7, а, если известно, что U = 240 В, ψu = 0, R = 60 Ом, С = 40 мкФ, f = 50 Гц.
Pешение
Находим:
xC = 1/(ωC) = 1/(2π fC) = 1/(2∙3,14∙50∙40∙10-6) = 80 Ом;
Z = R – jxC = 60 – j 80 = 100e – j 53° Ом;
|
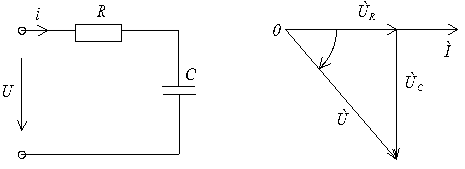
а) б)
Рис. 2.7
İ = Ù / Z = 240/(100e – j 53° ) = 2,4 e j 53° A;
ÙR = İ R = 60∙2,4 e j 53° = 144 e j 53° B;
ÙC = - İ jхC = 80∙2,4 e j 53° e - j 90° = 192 e – j 37° B.
Векторная диаграмма приведена на рис. 2.7, б. Ток в рассматриваемой цепи опережает приложенное к ней напряжение на угол φ = 53°.
Задача 2.8
Определить значение емкости С конденсатора, при котором в цепи рис. 2.8, а. установится резонанс токов. Найти входное сопротивление цепи при резонансе, а также токи ветвей. Построить векторную диаграмму токов. Напряжение сети U = = 120 В, а параметры цепи равны R = 3 Ом, XL = 4 Ом.

Решение
Условием резонанса токов является равенство модулей реактивных проводимостей ветвей: ВL = ВС. Для рассматриваемой схемы:

Отсюда

Входное сопротивление цепи можно найти иначе. Так как реактивные проводимости ветвей равны, а активная проводимость второй ветви:

то

Ток в неразветвленной части цепи:
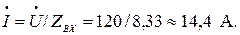
Ток ветвей:


Проверка: 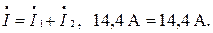
Из векторной диаграммы, изображенной на рис. 2.8, б, видно, что I2 = I1p, но их векторы направлены противоположно. Комплексный ток в неразветвленной части цепи I = I1a. Вектор тока İ совпадает по направлению с вектором входного напряжения  .
.
Задача 2.9
В сеть напряжением U = 120 В и частотой f = 50 Гц включена индуктивная катушка с сопротивлением R = 12 Ом и индуктивностью L = 66,2 мГн. Ее последовательная схема замещения изображена на рис. 2.9, а. Определить комплексный ток, значения полной, активной и реактивной мощностей. Построить топографическую диаграмму напряжений, треугольники сопротивлений и мощностей.
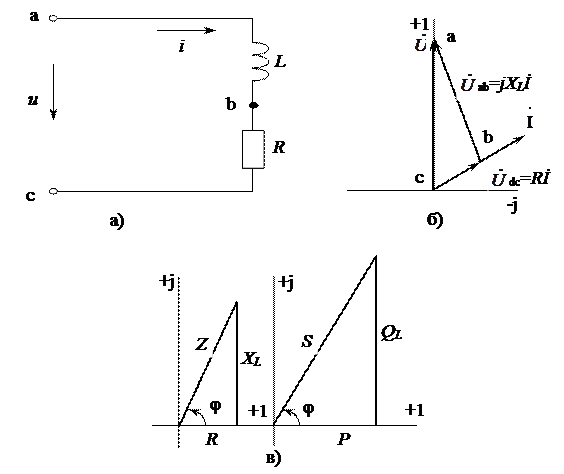
Рис. 2.9
Решение
Индуктивное сопротивление катушки: 
Комплексное сопротивление: 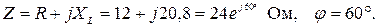
Комплексный ток: 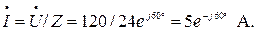
Комплексная мощность:
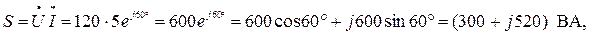
Откуда P = 300 Вт, Q = 520 вар, S = 600 ВА. Эти мощности могут быть найдены иначе.
Полная мощность 
Активная мощность 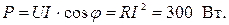
Реактивная индуктивная мощность 
Напряжение на активном элементе 
Напряжение на индуктивном элементе 
Вектор тока и топографическая диаграмма напряжений построены на рис. 2.9, б, треугольники сопротивлений и мощностей - на рис. 2.9, в.
Задача 2.10
В сеть напряжением U = 220 В и частотой f = 50 Гц включены последовательно соединенные батарея конденсаторов емкостью C = 290 мкФ и резистор с сопротивлением R = 5 Ом (рис. 2.10, а). Определить комплексный ток, полную, активную и реактивную мощности. Построить векторную диаграмму.

Рис. 2.10
Решение
Комплексное сопротивление: 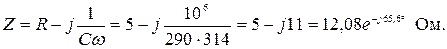
Комплексные напряжение и ток: 
Комплексная мощность:

Полная, активная и реактивная мощности:

Векторная диаграмма построена на рис. 2.10, б.
Вектор напряжения  совпадает с вектором тока, вектор напряжения
совпадает с вектором тока, вектор напряжения  отстает от вектора тока на 90°.
отстает от вектора тока на 90°.
Задача 2.11
Найти напряжение  cd в цепи (рис. 2.11, а), если параметры цепи равны R = XL = XC = 10 Ом, а Uab = 100 В. Построить топографическую диаграмму напряжений.
cd в цепи (рис. 2.11, а), если параметры цепи равны R = XL = XC = 10 Ом, а Uab = 100 В. Построить топографическую диаграмму напряжений.

а) б)
Рис. 2.11
Решение
Составляем уравнение по второму закону Кирхгофа для контура adca: 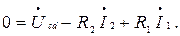
Отсюда 
Вектор напряжения  cd (выходное напряжение) опережает вектор напряжения
cd (выходное напряжение) опережает вектор напряжения  ab (входное напряжение) на угол 90°, их модули равны. Такая схема носит название фазосдвигающей. Построение топографической диаграммы напряжений (рис. 2.11) производим в следующем порядке:
ab (входное напряжение) на угол 90°, их модули равны. Такая схема носит название фазосдвигающей. Построение топографической диаграммы напряжений (рис. 2.11) производим в следующем порядке:
1) строим вектор входного напряжения  ab , общего для обеих параллельных ветвей;
ab , общего для обеих параллельных ветвей;
2) строим векторы токов İ1 и İ2;
3) принимаем  b = 0 и помещаем точку b в начало координат;
b = 0 и помещаем точку b в начало координат;
4) потенциалы точек c и d соответственно равны  с = jXLİ1 =
с = jXLİ1 =  cb ,
cb ,
 d=- jXCİ2 =
d=- jXCİ2 =  db, поэтому вектор
db, поэтому вектор  cd опережает вектор тока İ1 на угол 90°, а вектор
cd опережает вектор тока İ1 на угол 90°, а вектор 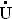 db отстает от вектора тока İ2 на тот же угол 90°;
db отстает от вектора тока İ2 на тот же угол 90°;
5) потенциал точки a равен  a=
a=  c + R1İ1 и
c + R1İ1 и  a=
a=  d + R2İ2 следовательно, вектор
d + R2İ2 следовательно, вектор
 ac= R1İ1 совпадает с вектором тока İ1, а вектор
ac= R1İ1 совпадает с вектором тока İ1, а вектор  ad= R2İ2 совпадает с вектором тока İ2;
ad= R2İ2 совпадает с вектором тока İ2;
6) входное напряжение  вх=
вх=  ab цепи равно сумме комплексных напряжений на реактивном и активном элементах каждой ветви.
ab цепи равно сумме комплексных напряжений на реактивном и активном элементах каждой ветви.
Из векторной диаграммы видно, что Ucd = Uab, но вектор  cd опережает вектор
cd опережает вектор  ab на 90°.
ab на 90°.
Задача 2.12
Цепь, состоящая из последовательно соединенных катушки с активным сопротивлением R = 50 Ом и индуктивностью L = 14,9 мГн, а также конденсатора емкостью С = 1,7 мкФ, подключена к источнику синусоидального напряжения, амплитуда которого неизменна, а частота может плавно изменяться в пределах 0< f0 <2 fрез. Построить частотные характеристики элементов и всей цепи, а также зависимость I (f), если U = 100 В.
Решение
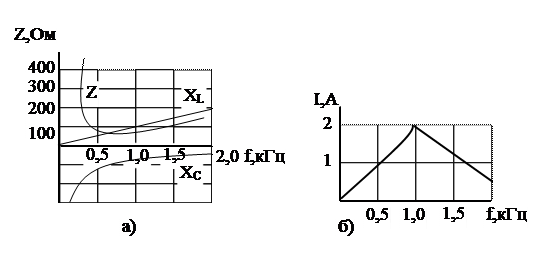
Рис. 2.12
Ответ: зависимости XL (f), XC (f) и Z (f) представлены на рис. 2.12, а, зависимость I (f) - на рис. 2.12, б; fрез = 1 кГц.
Задача 2.13
Катушка индуктивности в цепи источника синусоидального тока напряжения U1 = 100 В; комплексное выражение полной мощности  ВA.
ВA.
Определить мощность, потребляемую этой же катушкой, если включить ее в цепь источника постоянного напряжения, U2 = 100 В.
Ответ: P2 = 100 Вт.
Задача 2.14
 В цепи (рис. 2.14) u1= 10 sin(
В цепи (рис. 2.14) u1= 10 sin(  t+ 150 0) и
t+ 150 0) и
u2=- 10 cos  t.
t.
1.Представить u1(t) и u2(t) в комплексной форме.
2.Определить выражение для u(t) –результирующего напряжения.
3.Определить показания вольтметра, включенного между зажимами a и b.
Ответ: 1. u1 = Im[ 10 ej 150 ej  t]; u2=Im[ 10 e-j 90 ej
t]; u2=Im[ 10 e-j 90 ej  t];
t];
2. u = 10 sin (  t- 150 0);
t- 150 0);
3. Uab = 7,07 В.

 Задача 2.15
Задача 2.15




Дана цепь (рис. 2.15); I3=Re[ 2 ( 1 +j)ej  t], R1 = = 0,8 Ом, R2 = 2 Ом, R3 = 3 Ом.
t], R1 = = 0,8 Ом, R2 = 2 Ом, R3 = 3 Ом.
Определить действующие значения всех токов и напряжений источника.
Ответ: I1 = 5 A, I2 = 3 A, I3 = 2 A; U = 10 В.
Задача 2.16
 В цепи (рис. 2.16) i= 5 sin ( 628 t- 60 0) А, L = 0,01 Гн.
В цепи (рис. 2.16) i= 5 sin ( 628 t- 60 0) А, L = 0,01 Гн.
Определить:  , u(t), XL.
, u(t), XL.
Ответ:  =0,05sin ( 628 t- 60 0);
=0,05sin ( 628 t- 60 0);
u(t) =31.4sin ( 628 t+ 30 0);
XL=6,28 Ом.
Задача 2.17

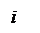 Цепь содержит только конденсатор (рис. 2.17) u= 100
Цепь содержит только конденсатор (рис. 2.17) u= 100  sin 10 3t, I = 1 A.
sin 10 3t, I = 1 A.
Определить: С.
Ответ: C = 10 мкФ.
Глава 3.
Дата добавления: 2015-10-24; просмотров: 347 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Лето кошмаров | | | Резонансные явления. |