
Читайте также:
|
1.1 Установить, дискретно или непрерывно пространство элементраных исходов, соответствующее следующим вероятностным экспериментам:
Е: подсчет числа вагонов, поступающих на станцию в течение суток;
Е: измерение времени ремонта вагона;
Е: подсчет числа перешивок стрелочного перевода;
Е: измерение времени движения поезда между двумя станциями;
Е: измерение массы вагона с грузом;
Е: подсчет числа отремонтированных вагонов в течение года;
1.2. Указать события, противоположные указанным событиям:
Е: подбрасывание двух монет
А – появление герба на первой монете;
В – появление двух гербов;
С – появление хотя бы одного герба;
D - одна монета упадет кверху гербом, вторая – кверху цифрой.
Е: определение числа дефектных деталей среди пяти изготовленных
А –среди изготовленных деталей есть хотя бы одна дефектная;
В – среди изготовленных деталей не менее двух дефектных;
С – среди изготовленных деталей более трех дефектных;
D - среди изготовленных деталей ровно три дефектных.
1.3 E: проверка качества трех изготовленных на станке деталей (каждая деталь может быть признана годной или дефектной). Построить пространство элементарных исходов данного эксперимента. Представить в виде совокупности элементарных исходов следующие события:
А – все проверяемые детали являются годными;
В – среди проверяемых деталей только одна дефектная;
С – среди проверяемых деталей – две дефектные;
D – все проверяемые детали – дефектные;
E – среди проверяемых есть хотя бы одна дефектная деталь;
F – среди проверяемых – не менее двух дефектных деталей;
G – деталь, изготовленная первой – годная.
В чем будут состоять события, противоположные к данным?
Выразить события  через события А, В, С, D.
через события А, В, С, D.
1.4 Электрические цепи составлены по схемам, приведённым на рисунке 1.1. Е: наблюдение за цепью в течение времени Т. Рассмотрим события: Аi = {безотказная работа элемента ei }, 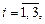 В = {безотказное функционирование электрической цепи}. Выразить событие В через события Аi.
В = {безотказное функционирование электрической цепи}. Выразить событие В через события Аi.
 а) а)
|
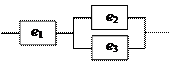 б) б)
|
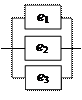 в)
в)
|  г)
г)
|
| Рисунок 1.1 – Логические схемы работы электрической цепи |
1.5 Е: из множества студентов БелГУТа случайным образом выбирается один студент. Рассмотрим события:
А = {выбранный студент окончил два курса обучения},
B = {выбранный студент проживает в общежитии},
C = {выбранный студент мужского пола},
D = {выбранный студент обучается на факультете УПП}.
В чём состоят события 





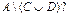
1.6 Студенту необходимо сдать три экзамена. Рассмотрим события: А 1 – сдача первого экзамена; А 2 – сдача второго экзамена; А 3 – сдача третьего экзамена. Записать выражения, соответствующие осуществлению следующих событий:
В – сдача всех трёх экзаменов;
С – сдача хотя бы одного экзамена из трёх;
D – сдача только первого экзамена;
F – сдача не более одного экзамена;
G – сдача двух экзаменов;
H – студент не сумел сдать только второй экзамен.
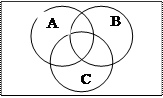 1.7 Е: В прямоугольной области Ω случайным образом выбирается точка. Определим события:
1.7 Е: В прямоугольной области Ω случайным образом выбирается точка. Определим события:
А = {выбранная точка принадлежит кругу А },
В = {выбранная точка принадлежит кругу В },
С = {выбранная точка принадлежит кругу С }.
|
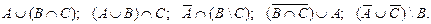
Дата добавления: 2015-09-01; просмотров: 52 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задание | | | ТЕМА 2. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ. МЕТОДЫ ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ |