Читайте также:
|
Поскольку в результате применения МСИ получают выборку значений представляющего случайную величину показателя надежности, то при построении имитационной модели возникает важный вопрос о правомерности распространения информации о выборочных характеристиках на истинные характеристики указанной случайной величины. Ясно, что чем большее число испытаний N включается в имитационный эксперимент, то есть чем больше объём выборки, тем точнее выборочное математическое ожидание, среднее квадратическое отклонение и другие характеристики. Однако увеличение N ведет к потерям дорогостоящего машинного времени. В этой связи N стремятся выбрать как можно меньшим при условии, что обеспечивается необходимая близость между выборочными и истинными характеристиками показателя надёжности. Применительно к математическому ожиданию того или иного показателя надёжности вопрос о точности МСИ решается на основе центральной предельной теоремы теории вероятностей следующим образом.
Пусть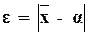 
- заданная погрешность, где 
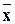- выборочное, α - истинное математическое ожидание представляющего случайную величину параметра надёжности. Зададимся достаточно близкой к 1 вероятностью Р и решим вопрос о том, каким должно быть число реализации N, чтобы с вероятностью Р погрешность в определении α не превышала e. Понятно, что рассмотрение этого вопроса без учета сходимости 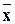к α по вероятности некорректно, поскольку 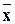является случайной величиной. сходящейся в вероятностном смысле к α при неограниченном увеличении N.
Поставленный вопрос решается с использованием конкретизирующего центральную предельную теорему неравенства
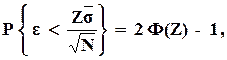(5.7)
где Ф(Z) - табулированная функция Лапласа, Z - ее аргумент. Из этого выражения найдем, что
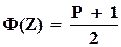
и по таблице Ф(Z) определим Z. Так как с вероятностью Р согласно выражению (5.7) должно быть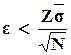 
, то
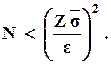
Следовательно, можно положить, что
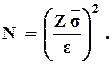(5.8)
Поскольку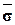 
заранее неизвестно, определение N осуществляется итеративно: задают, например, N1 = 100. После осуществления 100 реализации находят 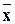и с его использованием - 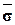. На основании (5.8) по заданному значению e, известным Z и 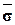проверяют, достаточно ли числа испытаний N1. Если достаточно, то полагают N = N1. В противном случае увеличивают N1, например, на 50 и снова осуществляют расчет 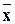, 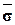и проверку достаточности испытаний. Расчёты проводятся на ЭВМ по соответствующей программе
Дата добавления: 2015-09-05; просмотров: 44 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Разыгрывание непрерывной случайной величин | | | Типовые моделирующие алгоритмы |