Главные напряжения и их основные схемы

Пусть в некоторой точке твердого тела N действует полное напряжение P_n. Этот вектор можно рассматривать как сумму трех взаимно перпендикулярных векторов P _x, P _y и P _z (рис. 2.4.)

В окрестностях точки N проведем три взаимно перпендикулярные площадки, нормалями которых являются оси координат x, y и z. Для каждой из этих площадок векторы P _x, P _y и P _z можно считать напряжениями, действующими на этих площадках. Каждый из векторов P _x, P _y и P _z можно представить как геометрическую сумму проекций на оси координат: одну нормальную и две касательные (например P _x = σ_x + τ _xy + τ _xz).

б)

а)

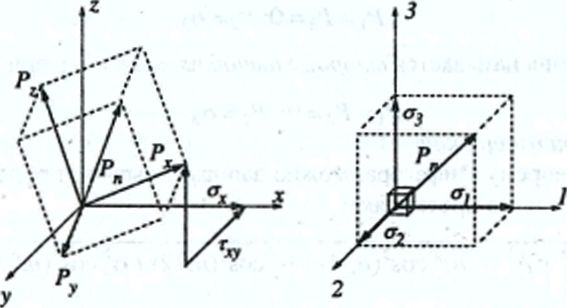
Рис. 2.4. Схема напряженного состояния: а – в обычных осях; б – в главных осях

Попробуем изменить (повернуть) направление осей координат и нормальных к ним площадок таким образом, чтобы направление осей, например N_x, совмещалось с направлением полного вектора напряжения Р_х. При этом касательные составляющие полного напряжения Р_x обозначенные на чертеже τ _xy, τ _xz обратятся в нуль. Согласно закону парности напряжений τ _xy = τ _yx = 0; τ_xz = τ _zx = 0; τ _yz = τ _zy = 0

Для случая, когда Р_х = σ _x, Р_y = σ _y, Р_z = σ _z, τ _xy = τ _xz = τ _yz = 0, введены обозначения нормальных напряжений σ ₁,σ ₂,σ ₃, которые названы главными. Направления, по которым действуют главные напряжения, называют главными и главными осями.

Существуют девять основных схем главных напряжений: две линейные, три плоские и четыре объемные (рис. 2.5.). Схема нагружений сильно влияет на основное свойство деформируемого металла – пластичность, т. е. на его способность подчиняться пластическим деформациям без признаков нарушения

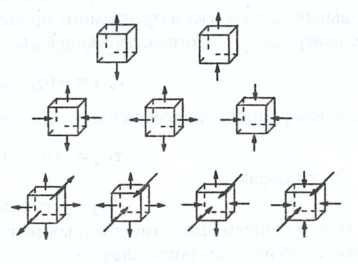
Рис 2.5. Основные схемы главных напряжений

Дата добавления: 2015-09-05