Испытание металлов на растяжение

В 1940-х гг. А.А. Ильюшиным была высказана гипотеза о том, что на зависимость обобщенного напряжения от обобщенной деформации σ _i(е _i) металла не влияет вид напряженного состояния. Эта гипотеза подтвер­ждена многочисленными экспериментами, и в ряде случаев постоянство (е _i) считают законом. Однако в реальных условиях деформируемые метал­лы сильно отличаются друг от друга по химическому составу, содержанию примесей, количеству дефектов кристаллического строения. Каждый из указанных факторов по-своему влияет на значение σ _s и вид σ _i(е _i). Поэтому говорить об одном характере кривой даже для одного марочного состава сплава можно лишь приближенно. «Нельзя продеформировать дважды один и тот же металл» - так можно перефразировать известное древнее изречение.

Причины различий свойств металлов и их изменений в процессе пла­стической деформации и термической обработки будут рассмотрены в сле­дующих главах.

Как же выглядит зависимость σ _i(е _i) полученная, например, из опытов на растяжение? Какие характеристики прочности и пластичности установ­лены этими испытаниями?

Рассмотрим одноосное растяжение.

Поведение металлов во время пластической деформации определяется их прочностью и пластичностью. Под прочностью обычно понимают спо­собность материала сопротивляться внешним силовым воздействиям, под пластичностью - способность пластически (необратимо) деформировать­ся без видимых признаков разрушения.

В качестве характеристик прочности и пластичности металлов исполь­зуют комплекс физико-механических свойств. Для их определения приме­няют различные виды механических испытаний, наиболее распространен­ным из которых является испытание на одноосное растяжение. Его выпол­няют на круглых или плоских в сечении образцах с диаметром (либо шириной и толщиной) и длиной рабочей части, соответствующими ГОСТ 1497-84.

Испытания проводят на разрывных машинах при комнатной, понижен­ной и повышенной температурах с различными скоростями растяжения. В результате опытов получают зависимость растягивающей силы от пере­мещения захватов машины, или, что одно и то же, при абсолютно жесткой машине, от удлинения образца Р (Δl). Для получения характеристик метал­ла, не зависящих существенно от геометрических размеров образца, ис­пользуют диаграмму условных напряжений σ _усл(ε _усл) или диаграмму ис­тинных напряжений σ (ε).

Для построения диаграммы σ _усл(ε _усл) напряжения, действующие в ме­талле во время растяжения, рассчитывают по соотношению

σ _усл = Р (Δl)/ F ₀, (2.7)

где Р (Δl) - текущее значение нагрузки; F ₀ - начальная площадь поперечно­го сечения образца.

Поскольку во время деформации площадь поперечного сечения F не­прерывно изменяется, то определение напряжений по соотношению (2.7) носит весьма приближенный, условный характер. Эта «условность» особенно сильно сказывается при больших деформациях и несущественна в начале диаграммы растяжения.

Относительные пластические деформации при построении диаграммы условных напряжений σ _усл(ε _усл) рассчитывают при растяжении по соотно­шению

ε _усл = Δl / l ₀, (2.8)

что также дает существенные отклонения от истинных деформаций, по­скольку длина рабочей части образца l ₀ постоянно изменяется. На рис. 2.6 показан вид цилиндрических и плоских образцов для испытаний на растя­жение, а на рис. 2.7 - диаграммы Р (Δl), σ _усл(ε _усл). В табл. 2.1 и 2.2 приве­дены стандартизированные размеры образцов.

Как видно, зависимости Р (Δl) и σ _усл(ε _усл) подобны друг другу, посколь­ку как параметр, так и сама вторая функция получены делением Р и Δl на константы F ₀ и l ₀. На этих кривых можно выделить характерные точки Р _пц(σ _пц), Р _упр(σ _упр), Р _т.в.(σ _т.в.), Р _т.н.(σ _т.н.), Р ₀₂(σ ₀₂), Р _в(σ _в).

Диаграмма истинных напряжений σ (ε) по внешнему виду отличается от диаграммы условных напряжений. Это вызвано тем, что истинные напря­жения и деформации металла при растяжении определяются следующим образом:

σ = P (Δl)/ F, (2.9)

ε = Δl / l, (2.10)

где F и l – текущие значения площади и длины рабочей части образца.

Рис. 2.6. Цилиндрические и плоские образцы для растяжения

Таблица 2.1

Размеры пропорциональных цилиндрических образцов для проведения испытаний на растяжение, мм

d 0	D	h	h 1	R	Длинные образцы l 0=10 d 0	Короткие образцы l 0=5 d 0
№	l0	l	№	l0	l
								16к
			2,5	1,5				17к
			2,5	1,5				18к
			2,5	1,5				19к

Примечание: L = l + 2 h + 2h ₁

Таблица 2.2

Размеры плоских образцов без головок, мм

a 0	b 0	l 0	Длинные образцы	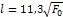Короткие образцы
№	l0	l	№	l0	l
						94к
						95к
						96к
						97к
						98к
						99к
0,5

Примечание: L = l + 2 h

Для определения значений F и l используют выражения, полученные из условия постоянства объема деформируемого металла: на всем протяжении испытаний:

ε = - ln(1- Ψ); (2.11)

F = F ₀(1- Ψ); (2.12)

до образования шейки на образце:

ε = - ln(1- ε _усл); (2.13)

F = F0(1- ε _усл); (2.14)

где Ψ - относительное сужение сечения в шейке образца.

На диаграмме истинных напряжений присутствуют те же характерные точки, что и на диаграмме σ _усл(ε _усл), за исключением σ _в. Напряжения σ _пц, σ _упр, σ _т.в., σ _т.н., σ ₀₂, σ _в, σ _р были приняты в обращение как характеристики прочности металла.

Предел пропорциональности σ _пц = P _пц/ F ₀. Эта величи­на определяет напряжения, ограничивающие область упругих деформаций. Обычно принято считать, что при σ < σ _пц выполняется закон Гука σ = Eε. Однако использование высокоточных испытательных машин показало, что в чистом виде закон Гука выполняется лишь до деформаций ε ≈ 10^-3 %, в связи с чем ввели понятия физического и технического пределов пропор­циональности. Физический предел наступает в тот момент, когда пласти­ческие деформации составят 1∙10^-3 %, или ε_пц = 0,00001; технический - ко­гда тангенс угла наклона кривой σ (ε) или σ _усл(ε _усл) изменит свое значение вдвое.

Предел упругости σ _упр = P / F ₀. Эта характеристика прочно­сти металла близка по значению и смыслу к пределу пропорциональности. Различие состоит в том, что σ _упр определяется тогда, когда остаточная де­формация образца достигнет 0,05 %, т.е. при ε = 0,0005.

Предел текучести. На рис. 2.7 видно, что некоторые из ме­таллов имеют на кривой Р (Δl) или σ (ε) участок, где пластическая деформа­ция происходит при постоянной силе. Этот участок называют площадкой текучести.

Начало этого участка представляет собой некоторый барьер - «зуб те­кучести», преодолев который металл деформируется при σ ≈ const. Нали­чие зуба текучести связывают с отрывом дислокаций от облаков примес­ных атомов или вакансий, вследствие чего их перемещение требует мень­ших напряжений.

На диаграммах с площадкой текучести определяют два предела текуче­сти - верхний и нижний: σ _т.в = P _т.в./ F ₀, σ _т.н. = P _т.н./ F ₀. Эти напряжения гово­рят о том, что в металле началась активная пластическая деформация. Ин­тервал напряжений σ _т.в - σ _пц называют иногда упругопластической зоной.

На кривых σ (ε) для тех металлов, у которых отсутствует в явном виде площадка текучести (рис. 2.7, II) за момент начала активной пластической деформации принимают напряжения, при которых пластическая деформа­ция составляет 0,2 %, т. е. при ε = 0,002. Для подобных материалов зона упругопластических деформаций простирается между σ ₀₂ и σ _пц.

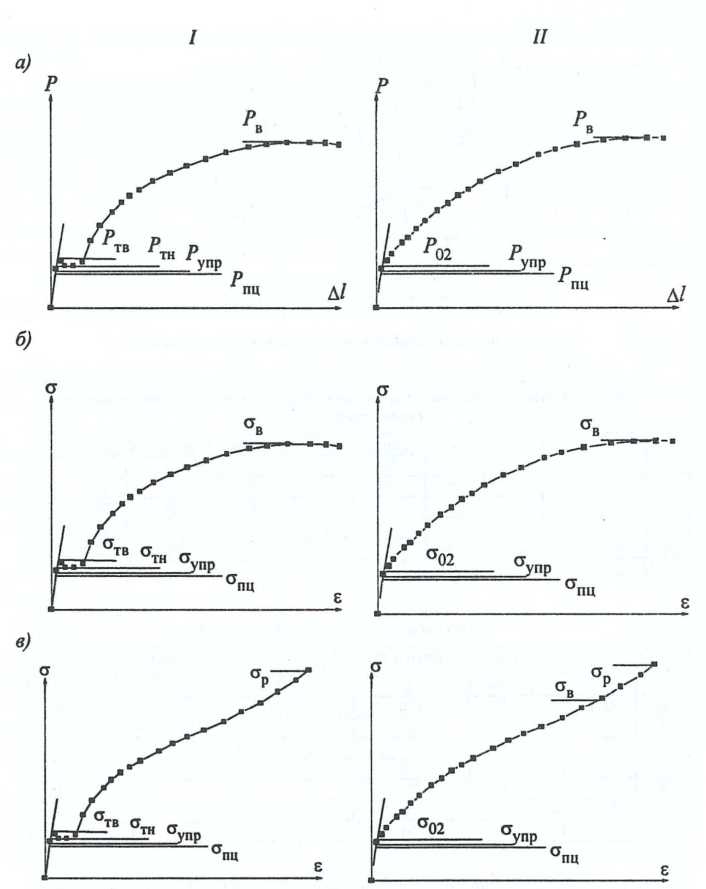
Рис. 2.7. Диаграммы растяжения с площадкой текучести (I) и без площадки текучести (II): а – индикаторная диаграмма P (Δl); б – диаграмма условных напряжений; в – диаграмма истинных напряжений

Характеристики металла σ _пц, σ _упр, σ _т.в., σ _т.н., σ ₀₂ мало отличаются друг от друга, если определять их по диаграммам условных или истинных напря­жений. Это связано с тем, что при малых значениях деформаций Δl или ε = Δl / l ₀ площадь поперечного сечения образца изменяется незначительно, т. е. F ≈ F ₀. Ситуация существенно меняется на участке деформационного упрочнения σ _т.н. < σ < σ _в, где деформация Δl или ε достигает больших значе­ний. В зоне активной пластической деформации и деформационного уп­рочнения истинные напряжения больше условных, σ > σ _усл, поскольку при растяжении F < F ₀ для той же деформации ε.

Известно, что деформационное упрочнение обусловлено изменением структуры из-за существенного увеличения плотности дефектов кристал­лического строения - вакансий, дислокаций, границ деформационного происхождения и др. Эти дефекты, располагаясь в объеме зерен опреде­ленным образом, образуют по мере возрастания деформаций клубковую, ячеистую, фрагментированную структуры. Упрочнение металла происхо­дит вплоть до разрушения образца.

Предел прочности (временное сопротивление) σ _в = P _в./ F ₀. Эта величина характеризует максимальные напряжения на кри­вой σ _усл(ε _усл). При напряжениях σ = σ _в в деформированном образце пла­стическая деформация локализуется в узкой области, образуется шейка, площадь сечения образца в этом месте уменьшается. Это снижение F тре­бует для продолжения деформации меньшей силы Р, в связи с этим кривая Р (Δl), которая записывается на испытательной машине, опускается ниже Р _в. Как следствие, и кривая условных напряжений σ _усл(ε _усл) опускается ниже σ _в. Вполне естественно, что подобного явления на диаграмме истин­ных напряжений σ (ε) не наблюдается, - происходит лишь изменение ин­тенсивности упрочнения.

Разрывная прочность (истинное сопротивле­ние разрыву) σ _р = P _р./ F _к. В выражении для σ _р F _к - площадь попереч­ного сечения образца в месте разрыва. Величина σ _р характеризует напря­жения, которые приводят к макроскопическому разрушению образца. На диаграмме истинных напряжений σ (ε) напряжения σ _р занимают наиболее высокое место.

При испытаниях металлов на растяжение определяют и характеристики пластичности - максимальное удлинение (в %) δ = ε _р∙100 и относительное сужение сечения образца в шейке после разрушения Ψ = (F ₀- F _к)/ F ₀.

В материаловедении для определения свойств металлов часто пользу­ются диаграммами условных напряжений, по которым можно найти значе­ния σ _пц, σ _упр, σ _в., σ _т, σ ₀₂, Ψ и δ. В практике пластической обработки метал­лов более важными являются диаграммы истинных напряжений σ (ε), так как, пользуясь ими, можно предсказать поведение металла в любом про­цессе пластической деформации - при прокатке, осадке, прессовании, во­лочении и т. д. Поскольку при растяжении σ ₂ = σ ₃= 0, то σ _i- = σ ₁, ε _i = ε и зависимость σ _i(ε _i) получается непосредственно из опытов на растяжение.

В табл. 2.3 представлены значения прочностных и пластических харак­теристик некоторых металлов, полученных из опытов на растяжение. Ме­ханические свойства во многом зависят от структурного состояния, в том числе от содержания примесей, размера зерна, вида обработки.

Таблица 2.3

Механические свойства некоторых металлов

Металл	σ пц, МПа	σ упр, МПа	σ 02, МПа	σ в, МПа	δ, %	Ψ, %
Al	25-30	28-40	30-42	88-100	30-60	85-95
Cu	45-50	50-60	70-76	210-230	30-55	80-90
Ag	40-60	42-66	45-76	180-240	35-60	80-95
Au	40-70	42-74	45-76	200-220	30-55	80-95
Fe	100-150	110-160	120-180	300-420	25-45	75-85
Ti	140-200	150-220	150-250	240-400	25-60	75-90
Mo	280-300	300-350	320-370	450-1100	15-30	50-65
W	650-700	660-720	700-810	850-1200	15-30	40-60
Сталь 45	140-160	150-180	160-200	300-380	20-35	60-70

Для того чтобы кривую σ (ε) можно было использовать для моделиро­вания любого из процессов пластической обработки металлов, ее нужно описать какой-либо математической формулой. Одним из критериев, влияющих на выбор физических гипотез и математических моделей, явля­ется простота. Такой подход согласуется с правилом бритвы, сформули­рованным монахом Оккамом около 700 лет назад. Этого правила придер­живаются многие исследователи, а звучит оно приблизительно так: «Нет нужды выискивать сложные трактовки какого-либо явления, если его мож­но объяснить более простыми причинами. Отсекай [бритвой] сложное, ес­ли можно обойтись простым». Иногда это правило называют критерием простоты. За более чем 250 лет исследования и аппроксимации кривых σ (ε) предложено несколько десятков формул, однако наиболее точно диа­грамму истинных напряжений описывают выражение:

σ = σ ₀ + αε ^β, (2.15)

а также полиномы вида

σ = σ ₀ + a ₁ ε, + a ₂ ε ² + a ₃ ε ³ +..., (2.16)

где параметры уравнений σ ₀, α, Р и α _i, определяются экспериментально.

Дата добавления: 2015-09-05