Связь между деформацией и напряжением

Под воздействием внешних сил все твердые тела изменяют свои разме­ры и форму. Происшедшие изменения, как известно, называют деформацией. Деформация представляет собой совокупность трех процессов – упругой деформации, пластической деформации и разрушения, которые в каждом из рассматриваемых объемов совершаются последовательно. Однако в силу вероятностного характера свойств различных микрообъемов эти процессы в деформируемом металле могут идти параллельно. Напри­мер, в образце разрушение происходит в наиболее слабом звене, в то время как в других частях может происходить только упругая деформация.

В процессе упругой деформации тело накапливает потенциальную энергию, которая при снятии нагрузки расходуется на восстановление раз­меров и формы тела. Многократные силовые воздействия на металл, при­водящие к упругой деформации, после окончания их действия не приводят к изменению размеров и формы тела.

Если внешние воздействия превосходят некоторый предел, характерный для каждого металла, то после окончания их действия размеры и формы тела не возвращаются в исходное состояние. Деформация становится необратимой. Видов необратимой деформации два – пластическая и вязкая. Пластическая деформация возможна при любых условиях воздействия внешних сил, тогда как вязкая наблюдается лишь при высоких температу­рах, когда выполняется условие Т_д ≥ Т_пл, а скорость деформации невелика (Т_д – температура деформации, К; Т_пл – температура плавления, К).

Чтобы понять сущность процессов, происходящих в металле во время деформации, необходимо иметь представление о тех изменениях состояния, которое дает наложение внешних сил.

Рассмотрим сплошное однородное изотропное тело произвольной фор­мы. Закрепим его в пространстве xyz, рассечем плоскостью на две части, одну из них отбросим, а направление секущей плоскости будем характери­зовать нормалью п.

Пусть dP – равнодействующая всех сил, действующая на элементарной площадке dF, выделенной в плоскости сечения на рис. 2.1. Тогда:

р= dP/dF (2.1)

полное напряжение на данной площадке dF.

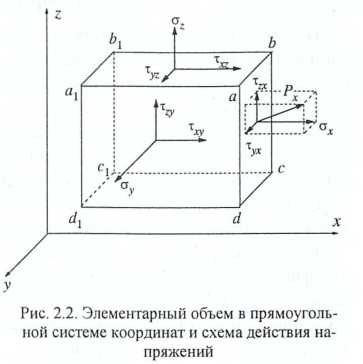
Напряжения в теле характеризуют обычно проекциями р на координат­ные оси. Для прямоугольной системы координат эти проекции показаны на рис. 2.2. На площадке abсd, перпендикулярной к оси х, действуют напря­жения σ_x, τ_yx, τ_zx Направление напряжения σ_x ┴ abсd, поэтому его называ­ют нормальным, а напряжения τ_yx, τ_zx ориентированные вдоль abсd и действующие соответственно вдоль осей x и z называют касательными. Всего на кубик металла, изображенный на рис. 2.2, действуют три нормальных напряжения σ_x, σ_y, σ_z и шесть касательных τ_xy, τ_xz, τ_yx, τ_yz, τ_zx, τ_zy.

Совокупность этих девяти величин носит название тензора напряже­ний и записывается в виде:

(2.2)

Индекс при букве σ обозначает направление нормальных напряжений. Первый знак индекса при букве τ указывает на направление касательных напряжений, а второй знак – на направление нормалей к соответствующим плоскостям рассматриваемого элементарного объема.

Если уменьшить объем куба, представленного на рис. 2.2, до размеров точки, то в этом случае тензор напряжений (2.2) будет отражать напряженное состояние в данной точке. Такая точка называется элементарным объемом, а вещество в нем – элементом системы.

Рис. 2.2. Элементарный объем в прямоугольной системе координат и схема действия напряжений

Рис. 2.1. Сечение тела плоскостью, перпендикулярной оси x

Напряжения, возникающие в металле от действия внешних сил, различ­ны в каждой точке, поэтому они являются функциями координат и при переходе от одной точки к другой изменяются на малую величину dσ или dτ.

Если тело находится в равновесии, то для каждого его элемента удовле­творяются шесть условий равновесия статики: суммы проекций сил на ка­ждую из осей и суммы моментов всех сил относительно каждой из осей равны нулю.

Зависимость, связывающая напряжения и деформации, которая исполь­зуется для решения задач теории упругости и пластичности, установлена опытным путем. Для решения таких задач пользуются соотношениями, выражающими закон Гука (2.3):

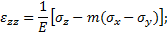
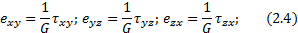
где Е, G - модули упругости и сдвига - основные упругие константы мате­риала; т - коэффициент Пуассона.

Величины Е, G, т связаны между собой соотношением

G = Е /2(1 + m), (2.5)

и их значения можно найти в справочниках по свойствам материалов. Модуль упругости Е можно трактовать как коэффициент пропорциональности между напряжением и деформацией при растяжении σ = εЕ, а модуль сдвига G – при кручении G = еτ.

Для пластической деформации связь между напряжением и деформаци­ей имеет более сложный вид. Если пренебречь изменением объема металла от упругой деформации, всегда сопровождающей пластическую, то эти зависимости можно записать в виде (2.6):

Здесь 1/2 - максимальное значение коэффициента Пуассона m, которое он достигает при переходе от упругой деформации к пластической; G' = E' /2(l + m') = Е'/3, где E' - модуль упругости металла при пластической деформации

2.2. ПЛОСКОЕ НАПРЯЖЁННОЕ СОСТОЯНИЕ

Дата добавления: 2015-09-05