Полиномиальная регрессионная модель и условия для ее определения

В.И.Жуков, Е.Ю.Тихонова

Определение регрессионной однофакторной математической модели (РОФМ) при традиционном (классическом) планировании активного эксперимента

Методические указания

Кострома

УДК 677.02.001.5

Определение регрессионной однофакторной математической модели (РОФМ) при традиционном (классическом) планировании активного эксперимента. Жуков В.И., Тихонова Е.Ю. –Кострома: КГТУ, 2007.-26с.

Методические указания предназначены для студентов направления 656000 специальности 260704 «Технология текстильных изделий» изучающих дисциплину «Методы и средства исследования механико-технологических процессов текстильной промышленности», а также для студентов других специальностей занимающихся математическим описанием технологических процессов. В методических указаниях изложена общая методика построения линейной модели объекта по результатам его экспериментальных исследований. Методические указания снабжены вариантами заданий, контрольными вопросами и всеми справочными статистическими материалами, необходимыми при выполнении расчетов.

Рецензент: доц. каф. ткачества КГТУ, к.т.н. Лазарев В.В.

© Костромской государственный технологический университет, 2007

1.Общие сведения

Полиномиальная регрессионная модель и условия для ее определения

Регрессионная математическая модель, получаемая по данным активного эксперимента с традиционным методом пла­нирования, имеет следующий полиномиальный вид:

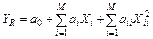. (1)

В этом полиноме отсутствуют члены 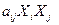, характеризующие взаимодействие факторов. Метод определения коэффициентов регрессии а₀, а_i, а_ii, т. е. оценки истинных значений коэффициентов регрессии α₀, α_i, α_iiна основе минимизации суммы квадратов отклонений экспериментальных значений Y от соответствующих значений Y_R, называется методом наименьших квадратов, или регрессионным анализом.

Применение метода наименьших квадратов правомерно при выполнении следующих условий:

1. Значения выходного параметра Yu в каждом u -м опыте матрицы планирования эксперимента представляют собой неза­висимые, нормально распределенные случайные величины.

2. Дисперсии выходного параметра в различных опытах матрицы (в различных точках факторного пространства) одно­родны или пропорциональны некоторой функции от Хи.

3. Значения уровней факторов не являются линейной комби­нацией от уровней остальных факторов.

4. Точность определения значений выходного параметра зна­чительно ниже точности определения величины уровня фактора.

При выполнении этих условий оценки коэффициентов регрес­сии будут состоятельными, несмещенными, эффективными и достаточными. Если одно или несколько из приведенных выше условий не будут выполняться, эффективность анализа значительно снижается, и по найденной модели могут быть получены неверные технологические выводы.

Дата добавления: 2015-09-05