|
Читайте также: |
Проверка этой гипотезы выполняется для каждого u -го опыта матрицы (например, для и= 1, когда X =2).
1) Проверка включает определение расчетного значения критерия WR по формуле
, (4)
где значение Q рассчитывается по формуле
; (5)
– при четном числе m, 
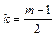– при нечетном числе m.
При подстановке значений в формулу (4) значения Y должны удовлетворять следующему условию: 
, т.е. для нашего случая 
. Значения qm-i+1 для i=1...k; m=3...50 приведены в прил.2 [1,прил.10]. Рассчитывая
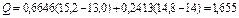
и подставляя это значение в формулу (3) получаем 
.
2) Сравнение расчетного значения WRi с табличным WT (прил.3), [1,прил.11], которое определяется для заданной доверительной вероятности и известного числа повторных опытов (измерений) т. Для рассматриваемого примера WT [ pD= 0,95; т = 5] = 0,762.
Так как расчетное значение критерия WR1 превышает табличноезначение WT для выбранной доверительной вероятности, то гипотеза о нормальном распределении случайных величин Y1vне отвергается.
В табл.1 приведены значения WR и для других опытов матрицы. Эти значения также превышают табличные, и поэтому первое условие о возможности применения регрессионного анализа удовлетворяется.
Дата добавления: 2015-09-05; просмотров: 54 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Первая операция – исключение резко выделяющихся данных. | | | Третья операция — проверка гипотезы об однородности дисперсий в опытах матрицы. |