Первая операция – исключение резко выделяющихся данных.

Рассмотрим эту при анализе первого опыта матрицы и =1, когда X ₁ =2, Y_{uv_max} =15,2, Y_{uv_min} = 13,0. Рассчитанные значения средних арифметических величин и дисперсий приведены в табл.1. Для исключения резко выделяющихся данных воспользуемся статистическим методом [1,с.26]. При этом методе определяются расчетные значения V_R – «критерия исключения резко выделяющихся данных выборки» для минимального и максимального значения, и полученные значения сравниваются с «критическим значением V_T критерия исключения резко выделяющихся данных выборки», которое определяется по специальной таблице (см. прил.1). Данный параметр называется также критерием Смирнова – Грабса.

При подозрении резко выделяющегося максимального значения Y _maxрасчетное значение критерия V_{R max}определяется по формуле

, (2)

а при подозрении резко выделяющегося минимального значения Y _minрасчетное значение критерия V_{R min}определяется по формуле

, (3)

где: –среднее арифметическое значение,

m – повторность измерений в опыте.

Используя формулы (1 и 2), определяем:

,

.

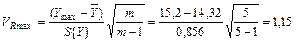По прил. 1 находим, что V_T [ p_D= 0,95; m = 5] = 1,869.

Так как V_{R max}=1,15< V_T =1,869и, V_{R min}=1,725< V_T =1,869, то рассмотренные значения Y_uvmax=15,2 и Y_uvmin= 13,0 не являются резко выделяющимися и остаются для дальнейшей статистической обработки.

В случае превышения расчетного значения V_R над табличным V_T, соответствующее значение Y_uv должно быть исключено из дальнейшей статистической обработки, а процедура отсева резко выделяющихся данных должна повторяться для оставшихся значений Y.

Дата добавления: 2015-09-05