Третья операция — проверка гипотезы об однородности дисперсий в опытах матрицы.

Так как число повторных опытов (т = 5) одинаково для всех опытов матрицы, то для проверки однородности дисперсий при­меняется критерий Кочрена (11.59), расчетное значение которого определяется по формуле

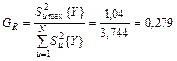. (6)

Расчетное значение G_R сравнивается с табличным значением G_T, которое определяют по прил. 4 в зависимости от числа опытов в матрице N и числа степеней свободы дисперсии 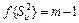для заданной доверительной вероятности p_D= 0,95. В рассматри­ваемом примере G_T [ p_D = 0,95; N =5; f = 5 — 1 =4] = 0,544. Так как G_R < G_T, то гипотеза об однородности дисперсий, т. е. равноточности и воспроизводимости опытов, не отвергается.

1.2.4.Четвертая операция — определение сред­ней дисперсии выходного параметра в опы­тах матрицы. Если в опытах матрицы дисперсии однородны и число повторных опытов одинаково, то средняя дисперсия опре­деляется по формуле

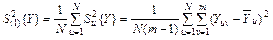. (7)

Число степеней свободы этой дисперсии равно

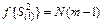. (8)

Средняя дисперсия характеризует средний разброс значений выходного параметра относительно его средних значений при каждом уровне факторов, т.е. ошибку опытов в эксперименте [2,III.2]. В рассматриваемом примере эта дисперсия, или, как ее называют, дисперсия воспроизводимости, равна:

.

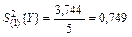Если число повторных опытов неодинаково при различных уровнях факторов, то для проверки однородности дисперсий используется критерий Бартлета, расчетное значение которого определяется по формуле [1,II.60].

Если случайные величины Y_u не имеют нормального рас­пределения, то применять критерий Бартлета не рекомендуется, так как он получен при условии нормального распределения этих величин.

При неоднородных дисперсиях или переходят к преобразова­нию значений выходного параметра, чтобы сделать дисперсии однородными, или применяют вариант метода наименьших квадра­тов с учетом величины дисперсии каждого опыта.

1.2.5.Пятая операция — определение подходя­щего вида регрессионной модели. Для опреде­ления подходящего вида регрессионной модели используют сле­дующую информацию:

1) вид взаимосвязи Y=f(X),устанавливаемый при теоре­тическом исследовании объекта или процесса;

2) графическую взаимосвязь 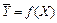между средними зна­чениями выходного параметра для каждого уровня факторов и значением фактора по данным эксперимента. При сопоставлении этого графика с графиками известных функций устанавливают вид уравнения;

3) характер изменения разделенных или неразделенных разностей первого порядка, определяемых по данным эксперимента.

Если в результате эксперимента получены следующие пары значений:

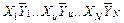, то разделенными разно­стями первого порядка называются величины

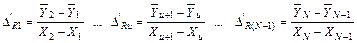
и неразделенными разностями первого порядка — величины

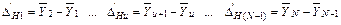. (9)

Неразделенные разности первого порядка используют, когда интервал варьирования факторов постоянный, т. е.

.

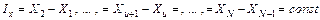В рассматриваемом примере интервал варьирования факторов постоянный и равен I_x = 4-2 = 6-4 = 8-6 = 10-8 = 2. Поэтому определяем неразделенные разности первого порядка по формуле (9):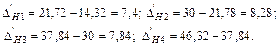

Ввиду малого различия неразделенных разностей первого порядка выходного параметра, не превышающего удвоенной ве­личины среднеквадратической ошибки эксперимента (2 S ₍₁₎{Y} = 1,724), можно считать, что они тождественны и поэтому для описания экспериментальных данных можно условно принять уравнение прямой линии

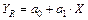(10)

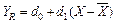или (11)

где 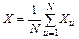. (12)

Использование уравнения (11) позволяет упростить ста­тистические расчеты при обработке экспериментальных данных, так как коэффициенты регрессии d₀ и d₁ не коррелированы. Коэффициенты регрессии d₀ и d₁ являются оценками истинных коэффициентов регрессии d ₀ иd ₁ в теоретической линейной зависимости вида .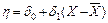

1.2.6.Шестая операция — определение коэффи­циентов регрессии. Если дисперсии выходного пара­метра для каждого уровня фактора однородны, то для определения коэффициентов регрессии в уравнении (III. 14) можно применять метод наименьших квадратов. Используя условие 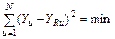, устанавливают следующие нормальные уравнения:

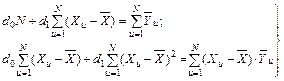(13)

Так как 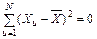, то, решая эти уравнения, получаем:

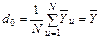; (14)

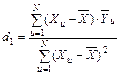. (15)

Определим по формулам (14) и (15) коэффициенты регрессии для рассматриваемого примера. Расчеты необходимых сумм сводим в табл.2.

Таблица 2

Промежуточные значения для расчета коэффициентов d ₁и d ₂

u	Xu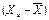
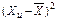
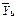
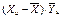
		-4		14,32	-57,28
		-2		21,74	-43,44
				30,00
				37,84	75,68
				46,32	185,28
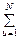
				150,20	160,24

По формулам (12, 14 и 15)находим:

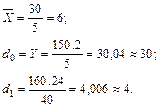
-Поэтому искомое уравнение имеет вид Y_R = 30 + 4 (X - 6)

или Y_R = 6 + 4Х. (16)

График этой функции изображен на рис.1

1.2.7.Седьмая операция — определение адекватности полученного уравнения. Для определения адекватности полученного уравнения используют критерий Фишера [2, 3], расчетное значение которого определяют по формуле

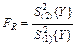, (17)

где: 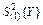-средняя дисперсия, или дисперсия воспроизводимости, определяемая по формуле (7); 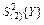- дисперсия, характеризу­ющая рассеивание средних экспери­ментальных значений 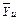относи­тельно прямой линии, определяемой по формуле (10).

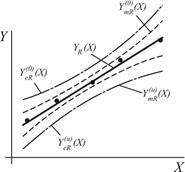Рис. 1. Линейная регрессионная однофакторная модель и ее доверительные интервалы

Дисперсия 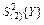характеризует точность аппроксимации зависимости 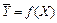, являющейсяпрямой линией и определяется по формуле

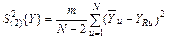. (18)

Число степеней свободы этой дисперсии 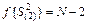. Под­ставляя в формулу (17) значения дисперсий из уравнений (7) и (18), получаем

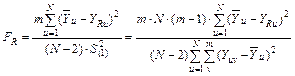. (19)

Расчетное значение F_R сравнивают с табличным значением критерия Фишера F_T, которое определяют по прил. 5 и при доверительной вероятности pD = 0,95 и числе степеней свободы дисперси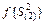й и 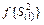. Если F_R < F_T, то гипотеза об адекватности линейного уравнения опытным данным не отвергается.

Расчет суммы в формуле (18) сведен в табл.3. Используя данные этой таблицы, находим 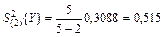. Подставляя найденные значения дисперсий в формулу (17), получаем .

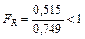Таблица 3

u	Xu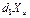
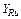
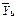
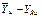
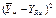
				14,32	0,32	0,1024
				21,72	-0,28	0,0784
				30,00	0,00	0,0000
				37,84	-0,16	0,0256
				40,32	0,32	0,1024
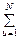
		-	-	150,20	-	0,3088

Промежуточные значения для расчета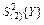

Так как F_R <1, то определяем обратное значение (17) отношения дисперсий, 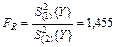и сравнивая его с табличным значением, которое равно 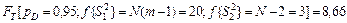. В рассматриваемом примере F_R =1,455< F_T =8,66, поэтому гипотеза об адекватности линейной модели не отвергается.

1.2.8.Восьмая операция — определение значимости коэффициентов регрессии и их доверительных интервалов. Для оценки значимости коэффициентов регрессии используется критерий Стьюдента [2,3], расчетное значение которого определяют по формуле

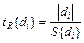, (20)

где S{d_i} – оценка среднего квадратического отклонения коэффициента регрессии d_i.

Для оценки дисперсий коэффициентов регрессии d₀ и d₁ в уравнении (10) используют формулы:

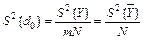, (21)

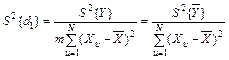. (22)

В формулы (21) и (22) входит дисперсия 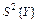, которая является сводной оценкой дисперсии случайной величины Y_u выходного параметра при условии линейной связи (11). Эта дисперсия определяется по формуле

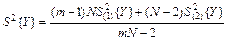. (23)

Число степеней свободы этой дисперсии

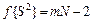. (24)

Подставив в формулу (23) ранее определенные значения 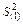и 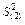, найдем сводную дисперсию случайной величины. Для рассматриваемого примера

.

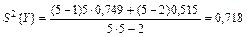По формулам (21) и (22) определяем дисперсии коэффициентов регрессии:

,

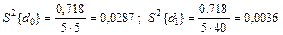и поэтому S{ d₀ }=0,169; S{ d₁ }=0,06.

Расчетные значения критерия Стьюдента определяем по фор­муле (20):

.

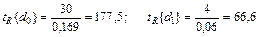По приложению 6 находим табличное значение критерия Стьюдента при условии, что доверительная вероятность p_D = 0,95 и число степеней свободы, определяемое по формуле (24), f {S²} =5×5-2=23. Следовательно, t_T [ p_D = 0,95; f = 23] = 2,07. Так как t_R {d₀} = 177,5 >> t_T = 2,07 и t_R{d₁} =66,6>> t_T = 2,07, полученные коэффициенты значимы и, сле­довательно, связь между Y и X значима.

Доверительные абсолютные ошибки коэффициентов регрессии вычисляем по формуле

.

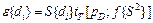В рассматриваемом примере эти ошибки равны: ; .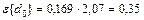

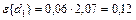Доверительные интервалы для истинных значений коэффициентов регрессии d₀ и d₁ в линейном уравнении (11) определяются неравенством

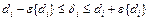. (26)

Для рассматриваемого примера доверительные интервалы коэф­фициентов регрессии при p_D = 0,95 следующие: 30 - 0,35 = 29,65 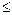d₀ 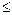30 + 0,35 = 30,35; 4 - 0,12 = 3,88 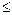d₁ 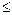4 + 0,12 = 4,12.

1.2.9.Девятая операция — определение дове­рительных интервалов средних значений выходного параметра при фиксированном значении фактора. Чтобы определить степень отклонения расчетных значений выходного параметра Y_Ru от истинного его значения при каждом уровне фактора Х_и, определяем доверительные ошибки e { Y_Ru } расчетного значения выходного параметра и доверительные интервалы среднего значения выходного параметра.

Доверительные ошибки расчетных значений выходного параметра для каждого уровня фактора рассчитываем по формуле

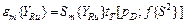, (27)

где 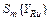— оценка среднего квадратического отклонения расчетного зна­чения выходного параметра Y_Ru для каждого значения Х_и,определяемая по формуле 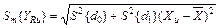. (28)

В рассматриваемом примере

.

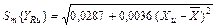Расчеты значений 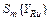для каждого, u -ro уровня фактора сведены в табл. 4.

Таблица 4

Расчет доверительных интервалов для средних значений выходного параметра

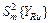
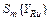
и	^Хи	(Xu-X)^2			em{YRu}	YRu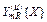
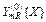
			861,4×10^-4	29,34×10^-2	0,61		13,69	14,61
			430,6×10^-4	20,75×10^-2	0,43		21,57	22,43
			287,2×10^-4	16,94×10^-2	0,35		29,65	30,35
			430,6×10^-4	20,75×10^-2	0,43		37,57	38,43
			861,4×10^-4	29,34×10^-2	0,61		45,39	46,61

В рассматриваемом примере табличное значение критерия Стьюдента (см. приложение 6) равно t_T [ p_D = 0,95; f{S²} = mN — 2 = 23 ] = 2,07. Подставляя это значение в формулу (27), получаем

.

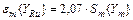В табл.4 приведены полученные значения 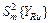, 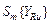и 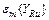для каждого уровня фактора. Зная ошибки расчетной величины, можно найти доверительные интервалы для истинных средних значений выходного параметра, исполь­зуя следующее неравенство:

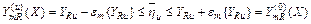. (29)

На основе приведенных в табл.4 значений границ доверительного интервала строим графики (см. рис.1) функци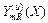й и 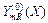. Графики этих двух функций образуют своеобразный «коридор». Любое сечение его прямой, параллель­ной вертикальной оси, соответствует доверительному интервалу, в котором с заданной вероятностью будет находиться истинное среднее значение выходного параметра 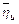. Легко заметить, что в этот «коридор» попадают средние экспериментальные значения .

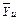Однако некоторые индивидуальные экспериментальные значения выходного параметра в него не попадают, так как интервалы построены для средних значений.

1.2.10.Десятая операция — определение доверительных интервалов для индивидуальных значений выходного параметра при каждом уровне фактора. Границы доверительного интервала для индивидуальных значений выходного параметра Y_uv при каждом уровне фактора Х_и определяются по формулам

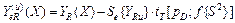, (30)

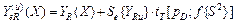, (31)

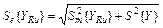. (32)

Используя значения 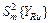из табл.4 и ранее опреде­ленные по уравнению (III.23) значения 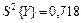и 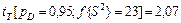, все расчеты верхней границы 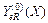и нижней границы 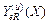искомой зоны по формулам (30) и (31) сводим в табл.5.

Таблица 5

Расчет доверительных интервалов для индивидуальных значений выходного параметра

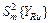
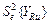
и	^Хи			Se{Yru}	YR(X)	tTSe{Yru}	YeR^(u)(X)	YeR^(0)(X)
		861,4×10^-4	8041,4×10^-4	0,897		1,86	12,14	15,86
		430,6×10^-4	7610,6×10^-4	0,872		1,81	20,19	23,81
		287,2×10^-4	7467,2×10^-4	0,864		1,79	28,21	31,79
		430,6×10^-4	7610,6×10^-4	0,872		1,81	36,19	39,81
		861,4×10^-4	8041,4×10^-4	0,897		1,86	44,14	47,86

Используя данные табл.5, строим графики функци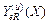й и 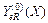(рис.1), которые являются доверительными границами зоны индивидуальных значений Y_uv выходного параметра. Вероятность попадания точек, соответствующих индиви­дуальным значениям выходного параметра, равна 0,95, т. е. из ста измерений выходного параметра при любом уровне варьирова­ния фактора 95 измерений попадают в эту зону и только пять не попадают.

Рассматривая индивидуальные значения Y_uv (см. табл.1) и границы зоны для каждого Х_u (табл.5), замечаем, что все индивидуальные измерения попали в доверительную зону, т.е. располагаются между 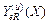и .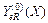

На этом заканчивается статистическая обработка данных рассматриваемого однофакторного эксперимента.

2.Методика выполнения расчета

В результате выполнения опытов, проведенных по плану активного классического (традиционного), однофакторного эксперимента, получены результаты, представленные в соответствующих вариантах «заданий».

Требуется:

1) Получить от преподавателя вариант задания.

2) Обработать данные однофакторного классического эксперимента. Произвести статистическую обработку данных, выполнив десять вышеизложенных операций.

3) При выполнении операций сделать соответствующие выводы.

4) По результатам вычислений построить графики зависимости от входного параметра:

- средних значений выходного параметра, полученных экспериментально;

- значений выходного параметра, полученных расчетным путем;

- доверительные интервалы для средних значений выходного параметра;

- доверительные интервалы для индивидуальных значений выходного параметра.

5) Написать уравнение регрессии в окончательном виде, описывающее зависимость выходного параметра Y от входного фактора X.

6) Проанализировать полученное уравнение, оценив весомость коэффициентов регрессии.

7) Сделать окончательные выводы.

3.Контрольные вопросы

1. Что означает термин «регрессионная» модель?

2. Какие методы отсева резко выделяющихся данных Вы знаете?

3. В чем заключается проверка гипотезы о нормальном распределении случайных величин?

4. Что означает «однородность дисперсий», и каким образом производится эта проверка?

5. По какой формуле производится расчет средней дисперсии в опытах матрицы?

6. В чем заключается разница расчета разделенных и неразделенных разностей?

7. Каковы правила выбора вида уравнения регрессии для описания исследуемого процесса?

8. В чем заключается смысл МНК – метода наименьших квадратов?

9. С помощью какого критерия, и как производится проверка адекватности полученного уравнения регрессии?

10. Как рассчитывается значение критерия Стьюдента, и для чего он используется при анализе значений коэффициентов уравнения регрессии?

11. Что показывают доверительные интервалы средних и индивидуальных значений выходного параметра?

4.ЗАДАНИЯ

Вариант 1

№ опыта	Входной параметр	Выходной параметр
u	X	Y1	Y2	Y3	Y4	Y5
		16.1	15.6	16.1	16.8	17.0
		22.6	24.1	23.0	22.4	23.2
		31.5	32.0	31.2	34.0	31.6
		43.2	43.1	42.3	48.0	44.5
		23.1	52.2	53.1	54.2	52.6

Вариант 2

№ опыта	Входной параметр	Выходной параметр
u	X	Y1	Y2	Y3	Y4	Y5
		6.6	7.2	7.0	8.0	6.2
		12.6	13.1	13.0	13.2	14.0
		22.6	24.1	21.0	22.1	20.2
		34.0	30.6	31.2	32.2	30.8
		43.0	42.5	42.0	48.9	49.0

Вариант 3

№ опыта	Входной параметр	Выходной параметр
u	X	Y1	Y2	Y3	Y4	Y5
		5.8	5.2	5.8	5.7	5.5
		14.3	13.1	12.8	12.6	14.0
		20.6	23.1	21.0	21.1	22.2
		29.0	32.0	31.5	28.5	32.0
		43.0	39.5	40.8	60.5	45.2

Вариант 4

№ опыта	Входной параметр	Выходной параметр
u	X	Y1	Y2	Y3	Y4	Y5
		15.2	14.8	13.0	14.6	14.0
		20.8	21.6	22.8	21.4	22.0
		28.8	30.0	31.2	29.2	30.8
		37.8	39.0	37.4	38.2	36.8
		47.2	46.6	45.0	46.8	46.0

Вариант 5

№ опыта	Входной параметр	Выходной параметр
u	X	Y1	Y2	Y3	Y4	Y5
		16.0	15.1	15.2	17.0	16.0
		19.5	20.1	18.2	18.2	19.1
		24.1	25.0	25.2	26.2	23.
		29.5	30.4	30.2	28.0	29.1
		32.6	33.2	34.2	34.1	32.1

Вариант 6

№ опыта	Входной параметр	Выходной параметр
u	X	Y1	Y2	Y3	Y4	Y5
		32.2	33.3	34.0	32.6	33.2
		39.1	40.2	40.0	38.0	41.0
		48.1	49.2	50.0	50.2	48.5
		57.1	60.2	58.1	56.2	60.4
		67.1	47.2	65.2	64.1	66.2

Вариант 7

№ опыта	Входной параметр	Выходной параметр
u	X	Y1	Y2	Y3	Y4

Вариант 8

№ опыта	Входной параметр	Выходной параметр
u	X	Y1	Y2	Y3	Y4

Вариант 9

№ опыта	Входной параметр	Выходной параметр
u	X	Y1	Y2	Y3	Y4

Вариант 10

№ опыта	Входной параметр	Выходной параметр
u	X	Y1	Y2	Y3	Y4

Вариант 11

№ опыта	Входной параметр	Выходной параметр
u	X	Y1	Y2	Y3	Y4
		76.3	76.8

Вариант 12

№ опыта	Входной параметр	Выходной параметр
u	X	Y1	Y2	Y3	Y4

Вариант 13

№ опыта	Входной параметр	Выходной параметр
u	X	Y1	Y2	Y3	Y4

Вариант 14

№ опыта	Входной параметр	Выходной параметр
u	X	Y1	Y2	Y3	Y4

Вариант 15

№ опыта	Входной параметр	Выходной параметр
u	X	Y1	Y2	Y3

Вариант 16

№ опыта	Входной параметр	Выходной параметр
u	X	Y1	Y2	Y3	Y4
		29.5	29.5
		34.5

Литература

1. Севостьянов А. Г. Методы и средства исследования механико-технологических процессов текстильной промышлен­ности: Учебник для вузов текстильной промышленности/ А.Г. Севастьянов —М.: Легкая индустрия, 1980.

2. Адлер Ю.П. и др. Планирование эксперимента при поиске оптимальных условий/ Ю. П. Адлер, Е. В. Маркова, Ю. В. Грановский —М.: Наука, 1965.

3. Налимов В.В., Чернова Н.А. Статистические методы планирования экстремальных экспериментов/ В.В. Налимов, Н.А. Чернова—М.:Наука, 1965.

Приложения

___________________________________________________________

Приложение 1

Критические значения V _T критерия исключения резко выделяющихся данных выборки

Повторности	РД
т	0,99	0,95	0,90
	1,414	1,412	1,403
	1,723	1,689	1,645
	1,955	1,869	1,791
	2,130	1,996	1,894
	2,265	2,093	1,974
	2,374	2,172	2,041
	2,464	2,237	2,097
	2,540	2,294	2,146
	2,606	2,343	2,190
	2,663	2,387	2,229
	2,714	2,426	2,264
	2,759	2,461	2,297
	2,800	2,493	2,326
	2,837	2,523	2,354
	2,871	2,551	2,380
	2,903	2,577	2,404
	2,932	2,600	2,426
	2,959	2,623	2,447
	2,984	2,644	2,467
	3,008	2,664	2,486
	3,030	2,683	2,504
	3,051	2,701	2,502
	3,071	2,717	2,537

Приложение 2

Коэффициенты q_m-i+1 используемые при проверке экспериментальных данных на нормальность с помощью критерия W, для m = 3... 25

m		0,4460	0,3060	0,2543	0,2148	0,1822	0,1630	0,1283	0,1046	0,0823	0,0610	0,0403	0,0200
	0,4493	0,3098	0,2554	0,2145	0,1807	0,1512	0,1245	0,0997	0,0764	0,0539	0,0321	0,0107
	0,4542	0,3126	0,2563	0,2139	0,1787	0,1480	0,1201	0,0941	0,0696	0,0459	0,0228	—
	0,4590	0,3156	0,2571	0,2131	0,1764	0,1443	0,1150	0,0878	0,0618	0,0368	0,0122	—
	0,4643	0,3185	0,2578	0,2119	0,1736	0,1399	0,1092	0,0804	0,0530	0,0263	—	—
	0,4734	0,3211	0,2565	0,2085	0,1686	0,1334	0,1013	0,0711	0,0422	0,0140	—	—
	0,4808	0,3232	0,2561	0,2059	0,1641	0,1271	0,0932	0,0612	0,0303	—	—	—
	0,4886	0,3253	0,2553	0,2027	0,1587	0,1197	0,0837	0,0496	0,0163	—	—	—
	0,4068	0,3273	0,2540	0,1988	0,1524	0,1109	0,0725	0,0359	—	—	—	—
	0,5056	0,3290	0,2521	0,1939	0,1447	0,1005	0,0593	0,0196	—	—	—	—
	0,5150	0,3306	0,2495	0,1878	0,1353	0,0880	0,0433	—	—	—	—	—
	0,5251	0,3318	0,2460	0,1802	0,1240	0,0727	0,0240	—	—	—	—	—
	0,5359	0,3325	0,2412	0,1707	0,1099	0,0539	—	—	—	—	—	—
	0,5475	0,3325	0,2347	0,1586	0,0922	0,0303	—	—	—	—	—	—
	0,5601	0,3315	0,2260	0,1429	0,0695	—	—	—	—	—	—	—
	0,5739	0,3291	0,2141	0,1224	0,0399	—	—	—	—	—	—	—
	0,5888	0,3244	0,1976	0,0947	—	—	—	—	—	—	—	—
	0,6052	0,3164	0,1743	0,0561	—	—	—	—	—	—	—	—
	0,6233	0,3031	0,1401	—	—	—	—	—	—	—	—	—
	0,6431	0,2806	0,0875	—	—	—	—	—	—	—	—	—
	0,6646	0,2413	—	—	—	—	—	—	—	—	—	—
	0,6872	0,1677	—	—	—	—	—	—	—	—	—	—
	0,7071	—	—	—	—	—	—	—	—	—	—	—
i

Приложение 3

Дата добавления: 2015-09-05