Читайте также:
|
Для матриц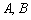 
и действительного числа 
справедливо следующее свойство:
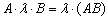
То есть числовой множитель можно (и нужно) вынести вперёд, чтобы он «не мешал» умножить матрицы.
Примечание: вообще говоря, формулировка свойства неполная – «лямбду» можно разместить в любом месте между матрицами, хоть в конце. Правило остаётся справедливым, если перемножаются три либо бОльшее количество матриц.
Пример 4
Вычислить произведение
Решение:
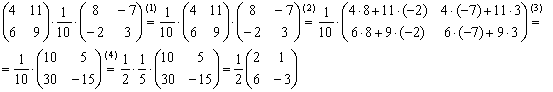
(1) Согласно свойству 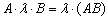перемещаем числовой множитель вперёд. Сами матрицы переставлять нельзя!
(2) – (3) Выполняем матричное умножение.
(4) Здесь можно поделить каждое число 10, но тогда среди элементов матрицы появятся десятичные дроби, что не есть хорошо. Однако замечаем, что все числа матрицы делятся на 5, поэтому умножаем каждый элемент на 
.
Окончательный ответ лучше оставить в виде 
, хотя, в принципе, годится и внесение дроби: 
. На технических тонкостях умножения матрицы на число я подробно останавливался на уроке Действия с матрицами.
Ответ: 
Маленькая шарада для самостоятельного решения:
Пример 5
Вычислить 
, если 
Решение и ответ в конце урока.
Какой технический приём важен в ходе решения подобных примеров? С числом разбираемся в последнюю очередь.
Прицепим к локомотиву ещё один вагон:
Дата добавления: 2015-08-27; просмотров: 56 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Немного о некоммутативности матричного умножения и единичной матрице | | | Как умножить три матрицы? |