
Читайте также:
|
! Помните, речь идёт об определителе! В самой матрице переставлять ничего нельзя!
Сыграем в кубик-рубик с определителем 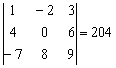 .
.
Поменяем первую и третью строку местами:
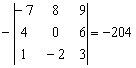
Определитель сменил знак.
Теперь в полученном определителе переставим вторую и третью строки:

Определитель ещё раз изменил знак.
Переставим второй и третий столбец:
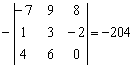
То есть, любая парная перестановка строк (столбцов) влечёт изменение знака определителя на противоположный.
Игры играми, но на практике такие действия лучше не использовать. Толку от них особого нет, а вот запутаться и допустить ошибку несложно. Однако приведу одну из немногих ситуаций, когда в этом действительно есть смысл. Предположим, что в ходе решения некоторого примера у вас нарисовался определитель со знаком «минус»:

Раскроем его, скажем, по первой строке:

Очевидное неудобство состоит в том, что пришлось выполнять лишние реверансы – ставить большие скобки, а затем их раскрывать (кстати, крайне не рекомендую выполнять подобные действия «за один присест» устно).
Чтобы избавиться от «минуса», рациональнее поменять местами любые две строки или любые два столбца. Переставим, например, первую и вторую строки:
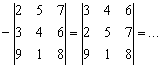
Теперь впереди помех нет, можно ехать дальше. Заядлых гонщиков ждёт кирпич: 29.
Выглядит стильно, но в большинстве случаев с отрицательным знаком целесообразнее разбираться другим способом (читайте дальше).
Рассмотренное действие опять же помогает лучше понять, например, некоторые свойства векторного произведения векторов или смешанного произведения векторов.
А вот это уже более интересно:
Дата добавления: 2015-08-27; просмотров: 139 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| При транспонировании матрицы величина её определителя не меняется | | | Из строки (столбца) определителя можно вынести общий множитель |