Читайте также:
|
В первую очередь коснёмся не свойств определителя, а как раз методов его рационального вычисления. Эти приёмы решения лежат на поверхности и понятны многим, но всё-таки остановимся на них подробнее. Предполагается, что читатель уже умеет достаточно уверенно раскрывать определитель третьего порядка. Как известно, данный определитель можно раскрыть 6-ю стандартными способами: по любой строке или любому столбцу. Казалось бы, без разницы, ведь ответ получится один и тот же. Но все ли способы одинаково легкИ? Нет. В большинстве случаев есть менее выгодные пути и более выгодные пути решения.
Рассмотрим определитель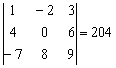 
, который я обильно покрыл татуировками ещё на первом уроке. В той статье мы подробно, с картинками разложили его по первой строке. Первая строка – это хорошо и академично, однако нельзя ли быстрее достичь результата? В определителе есть ноль, и, раскрывая его по второй строке либо по второму столбцу, вычислений заметно поубавится!
Разложим определитель по второму столбцу:
На практике нулевые элементы игнорируются, и запись решения принимает более компактный вид:
Задание 1
Раскройте данный определитель по второй строке, используя укороченную запись.
Решение в конце урока.
Если в строке (либо столбце) два нуля, то это вообще настоящий подарок. Рассмотрим определитель 
. Здесь два нуля в третьей строке, по ней и раскрываем:
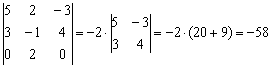
Вот и всё решение!
Особый случай, когда определитель имеет так называемый ступенчатый или треугольный вид, например: 
– в таком определителе все числа, расположенные ниже главной диагонали, равны нулю.
Разложим его по первому столбцу:
В практических заданиях удобно руководствоваться следующим правилом – ступенчатый определитель равен произведению чисел его главной диагонали:
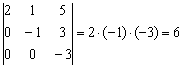
Аналогичный принцип справедлив и для ступенчатых определителей других порядков, например:
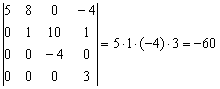
Треугольные определители появляются в некоторых задачах линейной алгебры, и их решение чаще всего оформляют именно так.
А если в строке (столбце) определителя находятся одни нули? Ответ, думаю, понятен. Мы ещё вернёмся к этому вопросу в свойствах определителя.
Теперь представим, что долгожданные баранки не положены в новогодний подарок. Так давайте же распотрошим нехорошего Санта-Клауса!
Здесь нет нулей, но всё равно существует способ облегчить себе жизнь. Данный определитель оптимальнее разложить по третьему столбцу, поскольку там самые маленькие числа. При этом запись решения принимает весьма лаконичный вид:
Резюмируя параграф, сформулируем золотое правило вычислений:
Определитель выгоднее раскрывать по ТОЙ строке (столбцу), где:
1) нулей побольше;
2) числа поменьше.
Естественно, это справедливо и для определителей высших порядков.
Небольшой пример для закрепления материала:
Задание 2
Вычислить определитель, раскрыв его по строке либо столбцу, используя при этом наиболее рациональный способ
Это пример для самостоятельного решения, оптимальное решение и ответ – в конце урока.
И ещё один важный совет: не комплексуйте! Не нужно «зацикливаться» на традиционном разложении по первой строке либо первому столбцу. Как короче – так и решайте!
Дата добавления: 2015-08-27; просмотров: 56 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойства определителя. Понижение порядка определителя | | | Свойства определителя |