
|
Читайте также: |
Здесь пропорциональны соответствующие элементы первой и второй строки:

Иногда говорят, что строки определителя линейно зависимы. Так как при транспонировании величина определителя не меняется, то из линейной зависимости строк следует и линейная зависимость столбцов.
В пример можно вложить геометрический смысл – если считать, что в строках записаны координаты векторов пространства, то первые два вектора с пропорциональными координатами будут коллинеарны, а значит, все три вектора – линейно зависимы, то есть компланарны.
В следующем примере пропорциональны три столбца (и, к слову, три строки тоже):
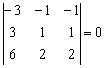
Здесь второй и третий столбец одинаковы, это частный случай – когда коэффициент пропорциональности равен единице
Перечисленные свойства вполне можно использовать на практике. Но помните, повышенный уровень знаний иногда наказуем;-) Поэтому, возможно, лучше раскрывать такие определители обычным способом (зная наперёд, что получится ноль).
Следует отметить, что обратное в общем случае неверно – если определитель равен нулю, то из этого ещё не следует, что его строки (столбцы) пропорциональны. То есть линейная зависимость строк/столбцов может быть и не явной.
Существуют и более очевидный признак, когда сразу можно сказать, что определитель нулевой:
Дата добавления: 2015-08-27; просмотров: 82 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Из строки (столбца) определителя можно вынести общий множитель | | | К строке определителя можно прибавить другую строку, умноженную на ненулевое число. При этом величина определителя не изменится |