Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Обратите внимание, что ! Это почти всегда так!

Действия с матрицами | Какие матрицы можно умножать? | Свойства определителя. Понижение порядка определителя | Эффективные методы вычисления определителя | Свойства определителя | При транспонировании матрицы величина её определителя не меняется | Если две строки (или два столбца) определителя поменять местами, то определитель сменит знак | Из строки (столбца) определителя можно вынести общий множитель | Если две строки (столбца) определителя пропорциональны (как частный случай – одинаковы), то данный определитель равен нулю | К строке определителя можно прибавить другую строку, умноженную на ненулевое число. При этом величина определителя не изменится |


Читайте также:
  1. E) переводится всегда существительным.
  2. E) переводится всегда существительным.
  3. E) переводится всегда существительным.
  4. E) переводится всегда существительным.
  5. Без смирения ни пост, ни молитва не спасут. Если будешь жить по своей воле и самочинию, то собьешься с толку. С родителями и со старшими надо обходиться почтительно
  6. Будьте братолюбивы друг к другу с нежностью; в почтительности ДРУГ ДРУГА ПРЕДУПРЕЖДАЙТЕ.
  7. Быть всегда готовым к его освещению

Таким образом, при умножении переставлять матрицы нельзя!

Если в задании предложено умножить матрицу на матрицу , то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.

Переходим к матрицам третьего порядка:

Умножить матрицу на матрицу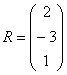

Формула очень похожа на предыдущие формулы:

А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:

Умножьте матрицу на матрицу

Вот готовое решение, но постарайтесь сначала в него не заглядывать!

Перед тем, как перейти к изучению следующего пункта, рекомендую отработать действия с матрицами на уроке Свойства операций над матрицами. Матричные выражения.

6) Действие шестое. Нахождение обратной матрицы.

Данная тема достаточно обширна, и я вынес данный вопрос на отдельную страницу.

Дата добавления: 2015-08-27; просмотров: 52 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Как умножить матрицы?| Как вычислить определитель?
mybiblioteka.su - 2015-2024 год. (0.007 сек.)