Читайте также:
|
Транспонируем матрицу:
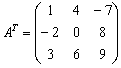
Примечание: действие подробно разобрано на уроке Действия с матрицами.
Согласно свойству, определитель транспонированной матрицы равен тому же значению: 
. Желающие могут убедиться в этом самостоятельно.
В ходу и более простецкая формулировка данного свойства: если транспонировать определитель, то его величина не изменится.
Запишем оба определителя рядышком и проанализируем один важный момент:
В результате транспонирования первая строка стала первым столбцом, вторая строка – вторым столбцом, третья строка – третьим столбцом. Строки стали столбцами, а результат не изменился. Из чего следует важный факт: строки и столбцы определителя равноправны. Иными словами, если какое-нибудь свойство справедливо для строки, то аналогичное свойство справедливо и для столбца! В действительности с этим мы уже давно столкнулись – ведь определитель можно раскрыть как по строке, так равноправно и по столбцу.
Не нравятся числа в строках? Транспонируйте определитель! Возникает только один вопрос, зачем? Практический смысл рассмотренного свойства невелик, но его полезно закинуть в багаж знаний, чтобы лучше понимать другие задачи высшей математики. Например, сразу становится ясно, почему при исследовании векторов на компланарность их координаты можно записать как в строки определителя, так и в столбцы.
Дата добавления: 2015-08-27; просмотров: 100 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойства определителя | | | Если две строки (или два столбца) определителя поменять местами, то определитель сменит знак |