Можно ли к матрице прибавить число?

Например: 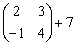. Ну, или наоборот: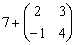

Нет. К матрице можно прибавить только другую матрицу, причём точно такого же размера.

Матрицу можно умножить на число. Но сложить их нельзя. Таковы правила игры.

Следует отметить, что допустимо сложение определителя матрицы с числом:

Результат вычисления определителя – число, а два числа суммируются без всяких проблем.

Вышесказанное, естественно, справедливо и для разности, ведь вычитание – это частный случай сложения.

Как на счёт того, чтобы плотно зависнуть у меня сегодня вечером? =) Практика показывает, что наибольшие трудности у студентов вызывает умножение матриц. Так наполним же кружки соответствующей информацией.

Повторим само правило. В статье Действия с матрицами я рассказал о том, какие матрицы можно умножать и привёл ряд наиболее распространённых примеров. Давайте рассмотрим операцию чуть подробнее и выделим два существенных пункта:

1) Смотрим на левую часть. Из первого урока нам известно, что матричное умножение возможно в том и только в том случае, если количество столбцов первой матрицы равно количеству строк второй матрицы.

2) Смотрим на правую часть и обращаем внимание на размерность результата – СКОЛЬКО строк и столбцов должно быть у итоговой матрицы.

Пример 1

Умножить матрицы

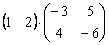
Решение: произведение существует, причём итоговая матрица состоит из 1-ой строки и 2-х столбцов:

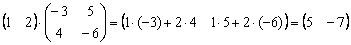
Ответ: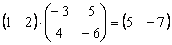

Пример 2

Умножить матрицы

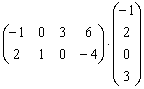
Это пример для самостоятельного решения.

Предложенные примеры не случайны. Они вроде бы просты, но у начинающих здесь нередко возникает путаница с размерами матрицы-результата. Поэтому читателям с небольшим опытом целесообразно переписать вышеприведённую формулу и особенно серьёзно отнестись к практическим примерам.

А по каким принципам составляются начинка (суммы произведений чисел), думаю, все уже поняли. Дополнительно возьмём на вооружение образную ассоциацию, которая поможет хорошо запомнить действие. Читаем следующий параграф:

Дата добавления: 2015-08-27