Читайте также:
|
Материал, по меньшей мере, частично вам знаком. Для тех, кто не знает термина:
Коммутативность = Перестановочность.
Обычные числа переставлять можно: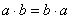 
, а матрицы в общем случае не перестановочны: 
. Собственно, подробная иллюстрация с конкретными примерами уже была дана в статье Действия с матрицами.
Рассмотрим некоторые исключения из правила, которые потребуются для выполнения практических задач.
Если у квадратной матрицы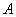 
существует обратная матрица 
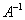, то их умножение коммутативно: 
Чтобы проверить, правильно ли найдена обратная матрица, нужно вычислить произведение 
либо произведение 
и убедиться в том, что получится единичная матрица 
. Конкретные примеры можно посмотреть в статье Как найти обратную матрицу?
Единичной матрицей называется квадратная матрица, у которой на главнойдиагонали расположены единицы, а остальные элементы равны нулю. Например: 
, 
и т.д.
При этом справедливо следующее свойство: если произвольную матрицу 
умножить слева или справа на единичную матрицу подходящих размеров, то в результате получится исходная матрица:
Как видите, здесь также имеет место коммутативность матричного умножения.
Возьмём какую-нибудь матрицу, ну, скажем, матрицу из предыдущей задачи: 
.
Желающие могут провести проверку и убедиться, что:
Единичная матрица для матриц – это аналог числовой единицы для чисел, что особенно хорошо видно из только что рассмотренных примеров.
Дата добавления: 2015-08-27; просмотров: 101 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Как возвести матрицу в квадрат? | | | Коммутативность числового множителя относительно умножения матриц |