Создание с помощью опционов безрисковых портфелей

Создать безрисковый портфель можно и с помощью опционов на продажу. Рассмотрим пример.

Пусть цена актива S равна 60 д.е., такова же и цена ис­полнения опциона на продажу. Срок действия опциона евро­пейского типа один месяц. Предположим, что к концу месяца с вероятностью 1/2 цена актива либо поднимется на 15 д.е., либо опустится на столько же. В первом случае опцион не­посредственно перед исполнением будет стоить 15 д.е., во втором не будет стоить ничего. Так как размах колебаний цен актива равен 30 д.е. и ровно в два раза превосходит колебания стоимости опциона перед испол­нением, то для создания безрискового портфеля держатель актива должен купить 2 опциона на продажу. Проверим, что портфель из актива и этих двух опционов действительно безрисковый.

В самом деле, в рамках рассматриваемой модели к концу месяца цена актива будет либо 75 д.е., либо 45 д.е. В первом случае владелец портфеля ничего не будет делать с куплен­ными им опционами на продажу, во втором случае продавец опционов выплатит ему по 15 д.е. за опцион. В обоих случаях к концу месяца портфель будет стоить 75 д.е. независимо от цены актива. Это и означает его безрисковость.

Определим цену опциона. Пусть банковская безрисковая ставка равна 10%. Современная стоимость портфеля равна 75/(1+0,1) =68,2 д.е. Но сейчас актив стоит 60 д.е. и поэтому два опциона вместе стоят 68,2-60 = 8,2 д.е. Следовательно, один опцион стоит 4,1 д.е. За такую цену оба опциона и должны быть куплены.

Проследим за капиталом покупате­ля опционов. Сначала у него был только актив стоимостью 60 д.е. Потом он купил два опциона, каждый по 4,1 д.е. Теперь у него денег -8,2 д.е. — долг за купленные опцио­ны, актив стоимостью 60 д.е. и два опциона, являющиеся фактически тоже активами, цена этих активов 8,2 д.е. Прежний актив и эти два опциона вместе образуют безрис­ковый портфель стоимостью 68,2 д.е. К концу месяца -8,2 д.е. уменьшатся по безрисковой ставке до -8,2 ∙(1+0,1) = -9 д.е., стоимость безрискового портфеля возрастет по безрисковой ставке до 75 д.е., всего у покупателя будет 75-9 = 66 д.е. — в точности как если бы его актив был безрисковым и его стоимость возросла бы по безрисковой ставке до 60∙(1+0,1) = = 66 Хеджирование полностью оградило покупателя от риска.

С помощью опциона на покупку можно застраховаться от излишне большого повышения цены на интересующий актив и обеспечить его приобретение по сегодняшней цене. Это делается следующим образом.

Купим опцион на покупку этого актива по цене испол­нения E и одновременно денежную сумму величиной 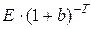, вложим в банк по безрисковой ставке b. К мо­менту исполнения опциона, т.е. через время T, эта сумма возрастет до E. Если цена актива к этому моменту не пре­высит E, то купим актив; иначе купим актив с помощью имеющегося у нас опциона на покупку.

Между стоимостями опционов на покупку и на продажу есть связь, известная как теорема паритета опционов.

Пусть C,P — стоимости соответственно опциона на по­купку и опциона на продажу и S,E — цена актива в момент продажи-покупки опционов и соответственно цена исполне­ния. Тогда

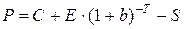(1)

где b — безрисковая ставка, T — время опциона.

Для доказательства этой формулы проведем два мыс­ленных эксперимента.

1.Приобретем актив по цене S и опцион на продажу с ценой исполнения E и стоимостью P, затратив всего S+P. Если цена актива в момент исполнения опциона превысит E, то актив сохраним, в противном случае актив продадим по цене E.

2.Купим опцион на покупку этого актива с ценой ис­полнения E и стоимостью C и одновременно вложим по без­рисковой ставке b денежную сумму величиной 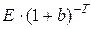, всего затратим 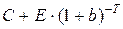к моменту исполнения опцио­на, т.е. через время T, эта сумма возрастет по безрисковой ставке до E. Если цена актива к этому моменту не превысит E, то купим актив; иначе купим актив с помощью имеюще­гося у нас опциона на покупку.

В рамках рассматриваемой модели оба эксперимента дают в конце один результат: если цена актива к моменту исполне­ния опциона превысит E, то у нас останется актив, иначе — де­нежная сумма E. Следовательно, и в начале этих экспери­ментов наш капитал должен быть одинаковым, т.е. должно быть 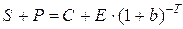, откуда и следует формула (1). Если цена исполнения опционов совпадает с сегодняшней рыночной ценой актива, то опцион на покупку дороже оп­циона на продажу.

Дата добавления: 2015-08-26