Другой подход к ценообразованию опционов

При биномиальной модели цена актива к концу n-го промежутка есть би­номиально распределенная величина, которую можно пред­ставить в виде 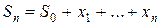, где случайные величины х_i, i = 1,..,n, — независимые одинаково распределенные слу­чайные величины, принимающие два значения 1,-1 с веро­ятностями 1/2 каждое. Пусть цена исполнения опциона равна S₀, т.е. равна рыночной цене актива в настоящий мо­мент 0. При этом предполагается, что S₀> n.

Доход держателя опциона при исполнении опциона есть

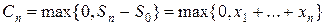
Ограничимся только одним периодом, тогда .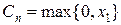

Ясно, что C — случайная величина. Так как торговля опционами носит массовый характер, то при определении их цены можно использовать средние числа. В частности, средний ожидаемый доход держателя опциона от одного опциона на покупку есть математическое ожидание случай­ной величины C₁, т.е.

Докажем, что это и есть «справедливая» цена опциона. При этом для упрощения примем, что безрисковая ставка равна 0. «Справедливость» цены означает, что продавец оп­циона сумеет обеспечить исполнение опциона и не более, т.е. никакой прибыли на выписке опциона он не заработает.

Далее переобозначим С=C₁ и x=x₁. [Докажем, что С = 1/2. Проще всего найти C, мысленно произведя над случайной ве­личиной x большое число опытов, скажем, 100. При этом в 50 опытах x примет значение 1 и потому] .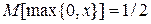

Покажем, как продавец опциона может распоря­диться этой суммой, чтобы обеспечить исполнение опциона. Он берет в банке заем величиной S₀/2-1/2, добавляет к этой сумме вырученную за продажу опциона 1/2 д. е. и на сумму S₀/2 покупает половину единицы актива. Итак, сей­час у него имеется [единица актива и] портфель, состоящий из долга банку, актива стоимостью S₀/2 и еще обязательства обеспечить исполнение опциона. Убедимся, что этот порт­фель безрисковый стоимостью 0.

В самом деле, если к моменту исполнения опциона цена актива увеличится на 1 д,е., то стоимость актива в портфеле увеличится до 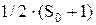[т.к. это половина актива], из этой суммы 1 д.е. пойдет дер­жателю опциона, а остальное, т.е. 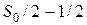— на погашение займа у банка. Если же цена актива упадет на 1 д.е., то дер­жателю опциона ничего не надо платить, а актив портфеля будет продан за 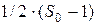- это в точности долг банку.

Докажем, что опцион не может стоить меньше чем С, в данном случае не может стоить меньше чем 1/2, т.к. иначе это не позволит продавцу обеспечить его исполнение, что означало бы крах всей опционной торговли. В самом, деле, если бы опцион стоил меньше и при этом продавец как-то умудрялся обеспечи­вать исполнение опционов, то покупатель имел бы строго положительный доход. Это позволило бы ему сгово­риться с продавцом, и они вместе бы построили «денежную машину»: продавец без конца выписывал бы оп­ционы, покупатель их покупал, а этот строго положитель­ный доход они бы делили, т.е. производили бы деньги из ничего. Но это невозможно.

Рассмотрим стоимость опциона в кон­це не одного расчетного периода, а многопериодного проме­жутка. Тогда 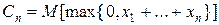[цена исполнения по-прежнему равна цене на момент продажи опциона].

При n > 10 согласно центральной предельной теореме сумма x₁ +...+ x_n распределена приближенно по нормальному закону с параметрами: математическое ожидание равно 0, дисперсия равна n. Следовательно, искомое математическое ожидание 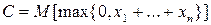равно

Дата добавления: 2015-08-26