Модель Блэка-Шоулс(з)а (Блека-Шолеса)

Модель первоначально разработана для оценки стоимости европейского опциона колл на акции, по которым не выплачиваются дивиденды. Следует заметить, что теоретические цены опционов, полученные по моделям, в силу неполноты учета экономических условий и их изменчивости, условности входящих статистических данных, как правило, отличаются от рыночных. Вместе с тем, принято считать, что если рыночная цена опциона сильно занижена относительно теоретической цены, то есть основание для его покупки.

Цены опционов определяются на рынке и зависят от ряда известных и неизвестных на момент его покупки параметров. К основным параметрам можно отнести:

• уровень цены исполнения;
• текущая цена базового инструмента;
• распределение вероятностей рыночной цены базового инструмента;
• размер процентной ставки;
• срок исполнения опциона.

Ф. Блэк и М. Шоулс (Black, Scholes) вывели следующую формулу

, (*)

где: с — премия европейского опциона колл (цена опциона);

S — цена спот акции в момент заключения контракта (текущая цена акции);

E — цена исполнения;

e^(-δt) – дисконтный множитель на срок t по непрерывной ставке δ;

t – срок до даты исполнения;

δ – непрерывная процентная ставка (сила роста), принятая для дисконтирования;

N (di) — функции нормального распределения;

, .

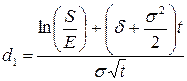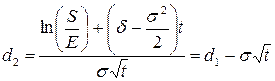σ^2 – дисперсия доходности акции (доходность измеряется в виде ставки непрерывных процентов);

Величина 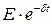представляет собой дисконтированную на момент покупки опциона цену исполнения.

Стоимость опциона зависит от степени вероятности того, что к моменту его истечения он окажется выигрышным. Вероятность в формуле (*) учитывается с помощью элементов N(d1) и N(d2). В модели в качестве вероятностного распределения цены акции принято логнормальное распределение.

Дата добавления: 2015-08-26