Теория Бартона — Прима — Слихтера для эффективного коэффициента распределения

Если затвердевание происходит медленно, как это предполагается в двух последних разделах, то концентрация примеси в жидкости одинакова, а концентрация примеси в затвердевшей части равна произведению концентрации примеси в жидкости и 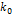, где 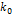— равновесный коэффициент распределения. Если же затвердевание нельзя считать медленным, то это не так.

Продвигающийся фронт кристаллизации оттесняет примесь быстрее, чем она успевает диффундировать в основной массе жидкости, вследствие чего впереди фронта кристаллизации образуется обогащенный слой 1). Концентрация примеси в таком слое больше концентрации примеси в основной массе жидкости, и скорее именно эта концентрация, а не концентрация примеси в основной массе жидкости определяет концентрацию примеси в затвердевшей фазе. При таком условии взаимосвязь между концентрацией примеси в твердой фазе 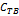и ее концентрацией в основной массе жидкости 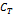можно охарактеризовать через эффективный коэффициент распределения 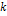, равный Ств/Сж. Во всей книге символ 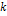используется для обозначения эффективного коэффициента распределения. Важно знать соответствующее значение 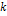, так как именно оно используется в расчетах процессов зонной плавки. Обычно оно находится между нулем и единицей. Но где именно? Эту задачу в конкретном случае вытягивания из расплава вращающегося кристалла проанализировали Бартон, Прим и Слихтер. Их подход к решению данной задачи основывался на принципах, описанных Нернстом в его теории кинетики гетерогенных реакций. Учитывая большую пользу уравнения Бартона — Прима — Слихтера, мы даем здесь его вывод. В основу вывода положено уравнение неразрывности применительно к числу атомов примеси на поверхности раздела между жидкой и твердой фазами. Эта поверхность считается стационарной при 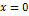, а рост кристалла рассматривается как вытекание жидкости в отрицательном к поверхности раздела направлении. При коэффициенте распределения меньше 1 примесь оттесняется растущим кристаллом, так что в жидкости возникает градиент концентрации. Концентрация примеси в жидкости у поверхности раздела продолжает увеличиваться до тех пор, пока не установится устойчивое состояние, при котором унос примеси от поверхности раздела путем диффузии, переноса жидкости и включения в твердую фазу не станет равен ее притоку к этой поверхности в затвердевающей жидкости. Если в жидкости нет течения и, следовательно, перенос примеси происходит только за счет диффузии, такое устойчивое состояние достигается тогда, когда коэффициент распределения станет . Однако жидкий расплав в контакте с остывающим кристаллом обычно не находится в таком состоянии. Как правило, в жидкости происходит то или иное движение вследствие конвекции тепла или некоторого принудительного перемешивания, так что значение 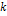находится между 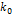и 1.

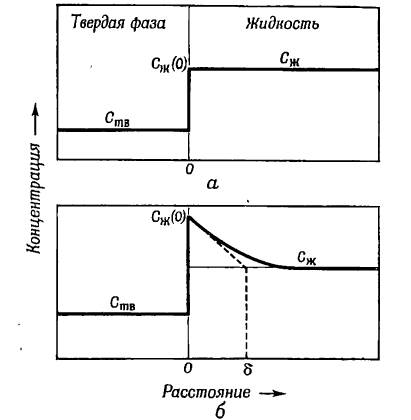
Фиг. 2.4. Концентрация примеси непосредственно впереди движущегося фронта кристаллизации при различных условиях роста кристаллов (по Бартону, Приму и Слихтеру). а — при равновесии (скорость роста пренебрежимо мала); б — при установившемся росте (с конечной скоростью).

Скорость любого потока в жидкости приближается к нулю у поверхности раздела во всех случаях, кроме потока, нормального к этой поверхности, т. е. порождающего рост кристалла. Независимо от характера потока в основной массе жидкости у поверхности раздела должна существовать такая область ламинарного течения, в которой скорость потока настолько мала, что перенос избыточной примеси от растущего кристалла будет осуществляться преимущественно путем диффузии. Вне этой области, называемой диффузионным слоем, который имеет толщину 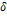, преобладает перенос вещества о результате течения жидкости, а концентрация примеси приближается к значению концентрации примеси в основной массе жидкости. Толщина 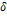изменяется приблизительно от 10 мкм при энергичном перемешивании до 1 мм при слабом перемешивании. Толщина диффузионного слоя зависит от коэффициента диффузии примеси, вязкости жидкости и режима ее течения. От скорости роста эта толщина зависит незначительно.

Дата добавления: 2015-08-20