Расчет распределения после многих проходов

Введение. Удобнее всего было бы иметь единое общее уравнение, выражающее концентрацию примеси в зависимости от расстояния при любом числе проходов через образец заданной длины.

Однако такого уравнения нет. Хотя основы зонной очистки просты, нетрудно видеть, что описать математически многократные операции зонной очистки не так просто. Тем не менее ряд математических методов подводит нас к конечной цели — выводу общего уравнения. Как и следовало ожидать, такие методы довольно сложны и их применение сопряжено с трудоемкими вычислениями. Эту задачу сравнительно просто решить с помощью быстродействующей вычислительной машины, причем ряд расчетных кривых распределения при зонной очистке уже опубликован в литературе. В заключительной части данного раздела кратко излагаются различные математические и расчетные приемы. В приложении к настоящей книге помещено много расчетных кривых распределения при зонной очистке. И хотя уже имеется много расчетных

данных, все же возможны случаи, когда приходится обращаться непосредственно к математическим вычислениям. Поэтому мы здесь остановимся на обоих путях. Основное дифференциальное уравнение, используемое во всех математических методах, было получено независимо Рейссом и Лордом. Это уравнение связывает изменение концентрации примеси в движущейся зоне с разностью между количествами поступающей в зону и уходящей из зоны примеси.

Уравнения (3.3а)

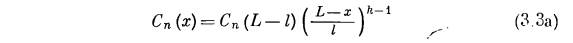
представляет собой уравнение нормальной кристаллизации.

Метод Лорда. Лорд получил точное выражение для концентрации примеси в функции расстояниям, отсчитываемого в длинах зоны от начала образца, и числа проходов . Оно справедливо лишь для образцов полубесконечной длины, т. е. не учитывает обратного отражения концентрирования примеси от конца образца. Таким образом, метод Лорда дает по сути дела формулу для многократного интегрирования дифференциального уравнения.

Полученное Лордом выражение записывается следующим образом:

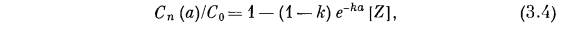
где 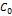— средняя концентрация примеси, считающаяся однородной. Здесь

если считать, что

Метод Рейсса. Рейсе получил аналитические решения, дающие непосредственно концентрацию после заданного числа проходов . Эти решения даются для образца полубесконечной длины в двух случаях: и . Они носят приближенный характер и, к сожалению, достаточно точны только для значений коэффициента распределения в интервале 0,9—1,1. С другой стороны, именно для таких значений 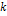обычно требуется много проходов, что предполагает очень трудоемкие вычисления. Вместо числа проходов и расстояния от начала образца он использует безразмерные переменные и , определяемые следующими соотношениями:

где —длина зоны, и

Правильная интерполяция и использование уравнений (3.12) и (3.13) позволяют отыскать с помощью этих кривых ответы почти на все практические задачи, когда величина 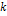близка к единице.

Пусть, например, и . Тогда значению соответствует число проходов .

Метод Хамминга. Это вычислительный метод, применимый к образцам конечной и полубесконечной длины с произвольным исходным распределением примеси. Образец делят на элементарные объемы, количество примеси выражает концентрацию примеси в них. Длина зоны берется равной целому числу длин таких объемов, скажем 4, 5 или более. Зона перемещается скачками из элементарного объема в соседний. При каждом скачке она оставляет в освобождаемом элементарном объеме затвердевшую примесь в количестве, равном ее концентрации в зоне, умноженной на 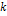. После каждого скачка примесь, поступившую из соседнего элементарного объема, прибавляют к примеси, переносимой зоной вперед, чтобы определить новую концентрацию в последней. Когда зона достигает конца образца и начинается нормальная кристаллизация, в вычислениях учитывается убывающий объем зоны. Когда же «затвердевает» последний элементарный объем, должна затвердеть вся примесь, что эквивалентно введению разрыва непрерывности. Примесь в зоне, достигшей конца образца, можно также распределить равномерно по длине последней зоны. Это будет соответствовать быстрой кристаллизации последней зоны, для которой эффективный коэффициент распределения 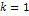равен единице. Наименьшее число элементарных объемов в зоне, для которого метод Хамминга еще дает приемлемую точность, равно двум. Вообще говоря, чтобы получить приблизительные результаты для нескольких проходов, можно прибегать к скачкам, по своей длине равным длине целой зоны, но при этом помнить, что подобный метод не позволяет учесть обратное отражение участка нормальной кристаллизации. Для скачков на половинную длину зоны при ошибка вычисления концентрации примеси может достигать 5%. При последующих проходах ошибка быстро возрастает. Таким образом, ради повышения точности при большом числе проходов целесообразнее пользоваться небольшими скачками, скажем на или 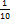длины зоны. По данным, полученным Хаммингом, было построено целое семейство расчетных кривых зонной очистки. При этом ширина скачка считалась равной 0,1 или 0,2 длины зоны, а интегрирование производилось по правилу трапеций для числа проходов, изменявшегося от 1 до . Такие вычисления дали следующие результаты:

Дата добавления: 2015-08-20