Сегрегация при нормальной кристаллизации

При равновесном затвердевании никакой сегрегации не возникает, потому, что имеется время для полной диффузии в твердой фазе. Если же диффузии в твердой фазе не происходит, а это ближе отвечает действительности, то при нормальной кристаллизации происходит сегрегация, степень которой зависит от условий переноса в жидкости. В этой связи можно установить три следующих случая:

1) полное перемешивание в жидкости (одинаковая концентрация примеси в ней);

2) частичное перемешивание жидкости;

3) отсутствие перемешивания в жидкости, так что перенос осуществляется только путем диффузии.

Рассмотрим эти случаи по порядку. Чаще всего встречается второй случай. Максимальное разделение при нормальной кристаллизации достигается при двух следующих условиях:

а) отсутствие диффузии в твердой фазе;

б) однородность концентрации в жидкости.

К этим условиям можно приблизиться путем выбора такой скорости затвердевания, которая будет велика по сравнению со скоростью диффузии примеси в твердой фазе, но мала по сравнению со скоростью диффузии примеси в жидкости. Когда же различие между коэффициентами диффузии примеси в жидкости и в твердой фазе незначительно и не позволяет сделать надлежащий выбор скорости затвердевания, жидкость нужно перемешивать, чтобы повысить эффективный коэффициент диффузии примеси в ней. В любом случае к условиям (а) и (б) физически можно приблизиться. Распределение примеси при нормальной кристаллизации можно охарактеризовать аналитически выражением

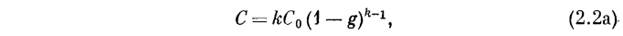
где 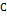— концентрация примеси в той части твердой фазы, где закристаллизовалась доля g исходной жидкости. Здесь предполагается, что выполняются упоминавшиеся выше условия (а) и (б), что соблюдены требования в отношении единиц, изложенные в разд. 2.2, и что величина к постоянна. Значение 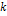в выражении (2.2а) равно 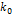только тогда, когда выполняются условия (а) и (б). Далее рассматривается вопрос об использовании эффективного коэффициента распределения 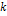, отличающегося от 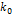. Если концентрация и доли g выражены в объемных единицах, то соответствующее уравнение запишется в виде

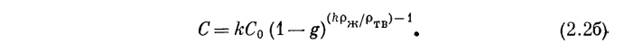
Уравнение (2.2а) имеет приближенный характер, так как она соблюдается не для всего интервала изменения 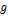. Во всякой реальной системе жидкость может достичь эвтектического или перитектического состава, после чего либо это уравнение утрачивает силу, либо величина к должна изменяться в зависимости от состава, поскольку по физическому смыслу она не может быть постоянной во всем этом интервале изменения .

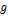На графике фиг. 2.3 построены кривые изменения концентрации примеси в зависимости от доли затвердевшей жидкости, рассчитанные по уравнению (2.2а) для различных значений параметра 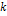. Здесь начальная концентрация принята равной единице, а величина 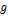доведена до 0,9. Степень сегрегации, о которой можно судить по наклону кривых, тем значительнее, чем больше величина 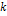отличается от единицы. Поскольку 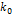— предельное значение эффективного коэффициента распределения для данной системы, условия затвердевания, для которых значение эффективного коэффициента распределения равно 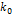, соответствуют максимальной сегрегации. Эти кривые показывают, что нормальная кристаллизация может быть весьма эффективным методом очистки, если абсолютное значение разности (1 — к) равно или больше приблизительно 0,5. Нормальная кристаллизация представляет собой элементарную стадию очистки путем многократной фракционной кристаллизации.

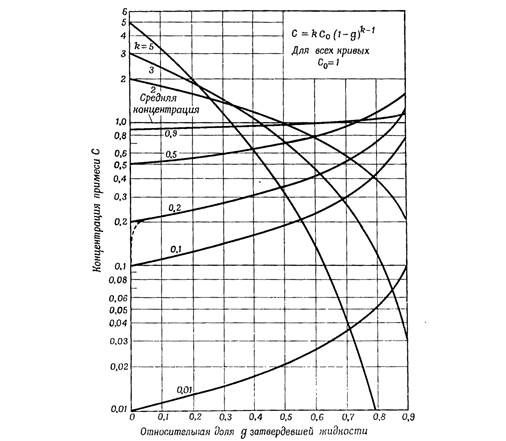
Фиг. 2.3. Кривые нормальной кристаллизации, характеризующие изменение концентрации примеси 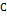в твердой фазе в зависимости от доли 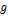затвердевшей жидкости. Кривые рассчитаны по уравнению (2.2а) для различных значений эффективного коэффициента распределения .

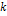Дата добавления: 2015-08-20