Конечное распределение

Уравнения конечного распределения. После многих проходов зоны распределение примеси приближается к установившемуся состоянию, или конечному (предельному) распределению, которое характеризует максимально достижимое разделение. С достижением этого состояния конвекционный поток примеси, вызываемый кристаллизационным действием зоны, встречает во всех точках образца равное противодействие обратного потока вследствие накопления примеси на конечном участке (смешивающее действие зоны). Уравнение конечного распределения получить легко. Пусть конечное распределение выражается функцией 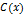. Если при проходе расплавленной зоны длиной через образец это распределение сохраняется неизменным, то в любой точке при затвердевании зоны из жидкой фазы в твердую переходит концентрация 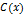, а концентрация в зоне равна 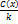. Но величина определяется также соотношением

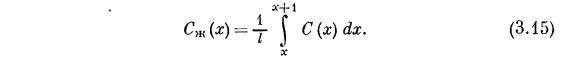
(Здесь предполагается, что площадь поперечного сечения зоны равна единице.) Поскольку 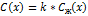, можно написать, что

Решением уравнения (3.16) является простое экспоненциальное выражение

где и — постоянные, определяемые соотношениями

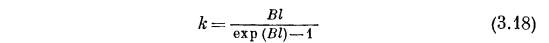
и

Здесь 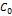— средняя концентрация примеси, a — длина образца. Уравнение (3.17) носит приближенный характер, так как оно утрачивает силу на конечном участке, по длине равном зоне,

в которой преобладает нормальная кристаллизация, поскольку распределение на этом участке отражается обратно на участок предшествующих зон. С удалением от конца образца сила этого противодействия убывает.

Удаление загрязненного конца образца при конечном распределении. Пусть в образце длиной после зонной очистки с использованием практически минимальной длины зоны установилось конечное распределение. Возникает вопрос, можно ли, укоротив образец до длины путем удаления загрязненного конца, добиться зонной очисткой вторичного конечного распределения? Ответ на этот вопрос зависит от того, как предполагается осуществить повторную очистку.

Если ее осуществлять исходя из укороченной длины образца как его новой длины, то повторная очистка никаких результатов не даст. Уже простая интуиция подсказывает, что повторная зонная очистка в подобных условиях очень незначительно отразится на концентрации при 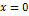. Само существование конечного распределения предполагает, что движущаяся зона во всех точках находится в равновесии с прилегающим к ней материалом. Зона «не знает», как далеко находится конец образца. Не считая небольшой складки, обусловленной нормальной кристаллизацией у конца образца при вторичном распределении, распределение примеси почти не изменится, если U выбрать за новую длину образца.

Дата добавления: 2015-08-20