Примеры. Объём конуса зависит от высоты и радиуса основания

Объём конуса зависит от высоты и радиуса основания

Объём V конуса зависит от высоты h и радиуса r, согласно формуле

Частная производная объема V относительно радиуса r

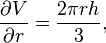
которая показывает скорость, с которой изменяется объём конуса, если его радиус меняется, а его высота остаётся неизменной. Например, если считать единицы измерения объёма 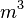, а измерения длины , то вышеуказанная производная будет иметь размерность скорости измерения объёма 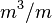, т.е. изменение величины радиуса на 1 м будет соответствовать изменению объёма конуса на .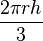

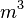Частная производная относительно h

которая показывает скорость, с которой изменяется объём конуса, если его высота меняется, а его радиус остаётся неизменным.

Полная производная V относительно r и h

и

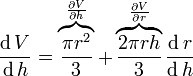
Различие между полной и частной производной — устранение косвенных зависимостей между переменными в последней.

Если (по некоторым причинам) пропорции конуса остаются неизменными, то высота и радиус находятся в фиксированном отношении k,

Это даёт полную производную относительно r:

Дата добавления: 2015-08-20