Читайте также:
|
Пусть функция 
имеет полные производные вплоть до 
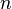-го порядка включительно в некоторой окрестности точки 
. Введём дифференциальный оператор
.
Тогда разложением в ряд Тейлора функции по степеням 
и 
в окрестности точки будет
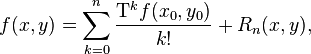
где 
— остаточный член в форме Лагранжа:
В случае функции одной переменной 
, поскольку для функции одной переменной частная производная тождественно равна полной. Аналогично формула распространяется на функции от любого числа переменных, меняется только число слагаемых в операторе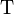 
.
Дата добавления: 2015-08-20; просмотров: 116 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Различные формы остаточного члена | | | Формула Тейлора для большого числа переменных |