Расчётная схема валов редуктора

8.1 Определяем реакции в подшипниках. Построение эпюр изгибающих и крутящих моментов (быстроходный вал):

Дано: F_t1 = 1108.3 H; F_r1 = 383 H; F_оп =474 Н; F_a1=80 Н; l_оп = 0,065 м; l_б = 0,045 м;

1) Определение реакции в подшипниках в вертикальной плоскости:

∑М₂ = 0

- F_оп·(l_оп+l_б)+ R_ау·l_б + F_r·l₁ +F_d1·d₁/2 = 0

R_ау=(474*(0,065+0.045)-383*0,025-1108.3*0,038/2)/0,045= 477.8Н

∑М₃ = 0

-F_оп ·l_оп+ R_ву·l_б + F_r·l_б/2+ F_а·d₁/2 = 0

R_ву=(474*0,065-383*0,045-80*0,045/2)/0,045=262.5 Н

Проверка: ∑У = 0

R_ау– F_r+ R_ву -Fоп=0

477.8+383+262.5- 474.3=0

0=0

Строим эпюры изгибающих моментов относительно оси Х в характерных сечениях 1…4, Нм

М_х4=0;

М_х3= - F_оп·l_оп=-52,6

М_х2= - F_оп·(l_оп +l_б)+ R_ax·l_б =176,3

М_х1^’= - F_оп·(l_оп +l_б+l₁)– R_ax·(l_б +l₁)+ R_бx·l₁=353,2

2) Определение реакции в подшипниках в горизонтальной плоскости:

∑М₃ = 0

F_t1·(l₁+l_б)- R_аx·l_б = 0

R_вx=(1509,3*(0,039+0,07)/0,07=2350,186 Н

∑М₂ = 0

- R_ах·l_б +F_t1 ·l₁= 0

R_aх=(-1509,3*0,039)/0,07=-840,895 Н

Проверка: ∑У = 0

-R_ах+R_вх – F_t =0

- 840,896+2350,186- 1509,3=0

0=0

Строим эпюру изгибающих моментов относительно оси У в сечениях 1...4:

М_у1=0; М_у4=0

М_у3= -52,6

М_у2- F_оп·(l_оп +l_б)+ R_aу·l_б =286,6

3) Строим эпюры крутящих моментов, Нм:

Мк = Мz = F_t1 ·d₁/2 = 54,33 Нм

4) Определяем суммарные радиальные реакции:

R_А = = 1867,68 Н

R_В = = 238,13 Н

Рисунок 8.1- Эпюра изгибающих моментов (быстроходный вал).

8.2 Определение реакций в подшипниках. Построение эпюр изгибающих и крутящих моментов (тихоходный вал):

Дано: F_t2 = 1509,3 H; F_r2 = 216,25 H; F_оп =3042,72 Н;

F_a2=498,25 Н; l_оп=0,017 м; l_T=0,141 м;

Fy=F_оп*sin30=1521,36 H; F_x= F_оп*cos30=2616,74 Н

1) Определение реакции в подшипниках в вертикальной плоскости:

∑М₃ = 0

F_м·l_оп - F_d1·d₁/2 + F_r·l_Т/2 -R_су·(l_Т/2+l_Т/2)= 0

R_ау=(2725*0.017-498,25*0,015+216,25*0,07)/0,141=498,93 Н

∑М₁ = 0

F_м ·l- R_ву·l_Т /2- F_а·d₁/2 - F_r·l_б/2= 0

R_ву=(2725*0,158-498,25*0,015-216,25*0,07)/0,07=282,68 Н

Проверка: ∑У = 0

-R_dу+ R_ву - F_r =0

-498,93+282,68-216,25=0

0=0

Строим эпюры изгибающих моментов.

М_х4=0; М_х3=0

М_х2= F_м·(l_оп +l_Т/2)- R_x·l_Т /2=20,24

М_х1= F_м·l - R_x·l_Т + F_t·l_Т/2=197,57

2) Определение реакции в подшипниках в горизонтальной плоскости:

∑М₃ = 0

F_х·(l_оп+l_Т)- R_сx·l_Т + F_t1 ·l_Т/2= 0

R_сx=(2616,74*(0,017+0,141)+1509*0,07/0,141=3670,64 Н

∑М₂ = 0

-F_х·l_оп – R_dх·l_Т +F_t1 ·l_Т/2= 0

R_dх=(-2616,74*0,017)+1509,3*0,07/0,141=433,69 Н

Проверка:

∑Х = 0; F_x-R_cx+F_t2-R_dx=0

2616,74-3670,6+1509,3 – 433,69=0

Строим эпюры изгибающих моментов относительно оси Х в характерных сечениях 1…4, Нм

М_у3=0; М_у4=0

М_у2= F_м(l_оп+l_t/2) – R_x*l_т/2=20,24

М_у1= F_м·l_оп– R_x*l_т+ F_t1 ·l_Т/2=197,57

3) Строим эпюры крутящих моментов:

Мк = Мz = F_t1 ·d₁/2 = 123,76 Нм

4) Определяем суммарные радиальные реакции:

Rс = 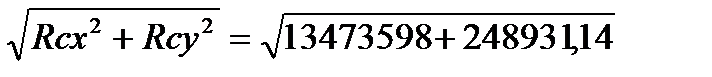= 3705,40 Н

Rд = 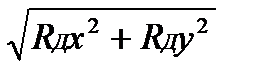= = 518,69 Н

Рисунок 8.1- Эпюра изгибающих моментов (тихоходный вал).

Дата добавления: 2015-08-17