|
Читайте также: |
№14. Найти 
, используя правило Лопиталя.
Решение:
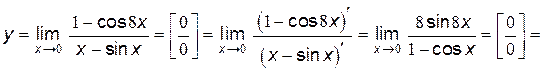
№15. Найти промежутки возрастания и убывания, точки максимума и минимума функции, промежутки вогнутости и выпуклости, точки перегиба графика функции 
.
Решение:
Находим критические точки функции из равенства 
:
.
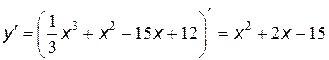– критические точки функции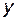 
.
Эти точки разбивают область определения функции 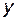на промежутки 
, 
, 
. Определим знак производной 
на каждом их этих промежутков:
 |
Т.о., функция 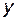возрастает на промежутках и и убывает на промежутке . При этом точка 
является точкой максимума функции, а точка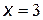 
– её точкой минимума.
Для определения промежутков выпуклости и вогнутости находим вторую производную и приравниваем её к нулю:
.
.
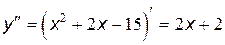Т.о., точка графика с абсциссой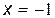 
является подозрительной на перегиб. Точка 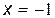разбивает область определения функции 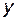на промежутки 
и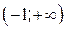 
. Определим знак второй производной 
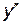на каждом их этих промежутков:
 |
Т.о., график функции 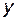является выпуклым на промежутке и вогнутым на промежутке .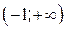
Поскольку 
, то точка 
является точкой перегиба графика функции.
Дата добавления: 2015-08-20; просмотров: 55 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение. | | | Формулы и символы |