
|
Читайте также: |
Функция  определена и непрерывна на интервалах
определена и непрерывна на интервалах 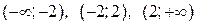 , где она задана непрерывными элементарными функциями. Следовательно, разрыв возможен только в точках
, где она задана непрерывными элементарными функциями. Следовательно, разрыв возможен только в точках 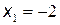 и
и 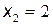 .
.
Для точки 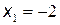 имеем:
имеем:
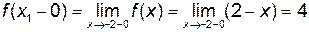 ,
, 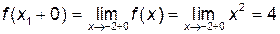 ,
, 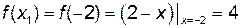 . Так как
. Так как 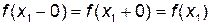 , то функция
, то функция  в точке
в точке 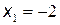 является непрерывной.
является непрерывной.
Для точки 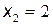 имеем:
имеем:
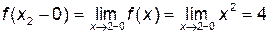 ,
, 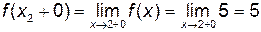 ,
, 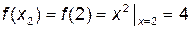 , т.е. функция
, т.е. функция  в точке
в точке 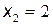 имеет разрыв первого рода. При этом скачок функции в точке
имеет разрыв первого рода. При этом скачок функции в точке 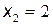 равен
равен 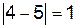 .
.
График функции имеет вид:
 |
№13. Найти производную функций
а) 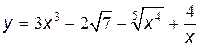 .
.
Решение:
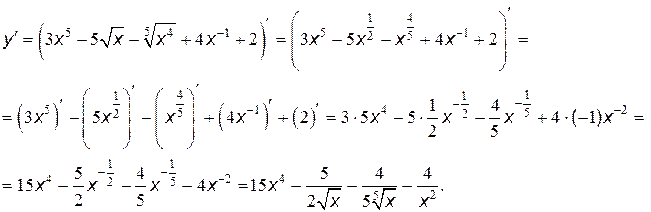
б) 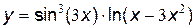 .
.
Решение:
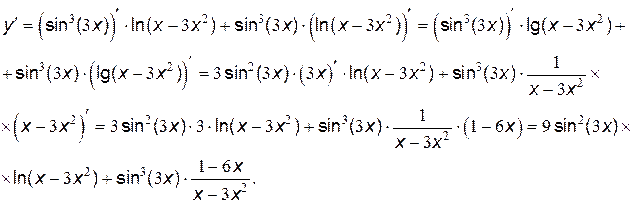
в)  .
.
Дата добавления: 2015-08-20; просмотров: 53 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Найти предел используя правило Лопиталя. | | | Решение. |