Найти предел используя правило Лопиталя.

1.		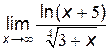6.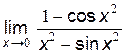
2.		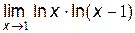7.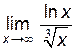
3.		8.
4.		9.
5.		10.

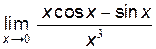
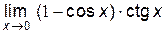
№15 Найти промежутки возрастания и убывания, точки максимума и минимума функции, промежутки вогнутости и выпуклости, точки перегиба графика функции:

1.		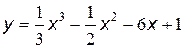6.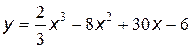
2.		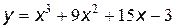7.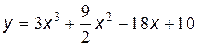
3.		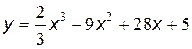8.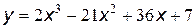
4.		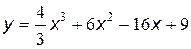9.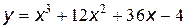
5.		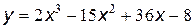10.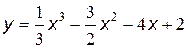

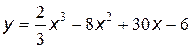
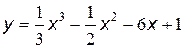
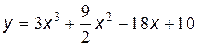
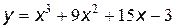
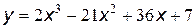
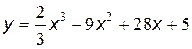
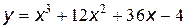
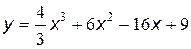
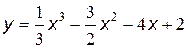
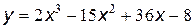
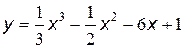
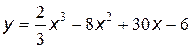
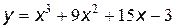
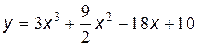
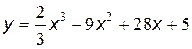
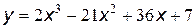
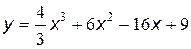
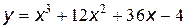
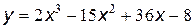
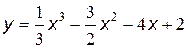
Рекомендации к решению:

№6. Даны векторы 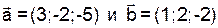. Вычислить .

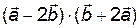Решение:

.

.

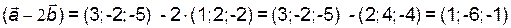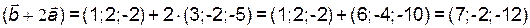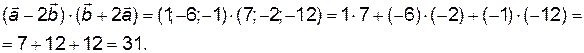
Ответ: 31.

№7. Найти угловой коэффициент прямой, проходящей через точк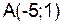и и .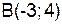

Решение:

Составим уравнение прямой AB, как уравнение прямой проходящей через две точки:

.

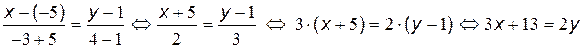Выражаем 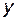: 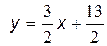. Угловым коэффициентом является коэффициент при : .

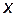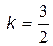Ответ: .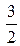

№8. Даны координаты вершин треугольника 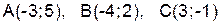. Найти площадь треугольника .

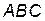Решение:

Площадь треугольника АВС равна 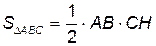, где 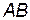– сторона треугольника, 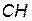– его высота.

Найдём длину стороны AB: .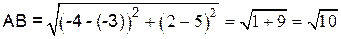

Составим уравнение прямой AB, как уравнение прямой проходящей через две точки:

.

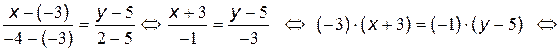
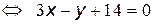Найдём длину высоты СН как расстояние от точки С до прямой АВ:

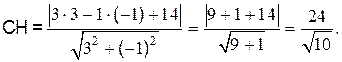
Окончательно получаем: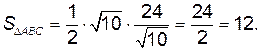

Ответ: 12.

№9. Найти расстояние от точки 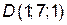до плоскости, проходящей через точк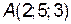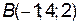и , и :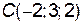

Решение:

Уравнение плоскости, проходящей через три точки, имеет вид:

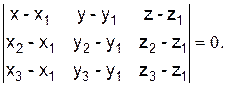
Так как наша плоскость проходит через точки 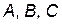, то её уравнение будет: 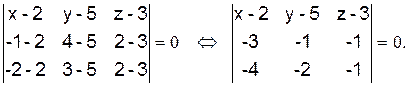Вычислим этот определитель, разложив его по элементам первой строки:

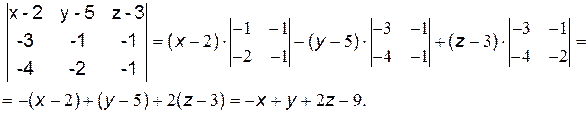
Таким образом, уравнение плоскости запишется в виде: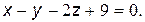

Расстояние от точки 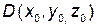до плоскости 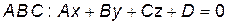находится по формуле:

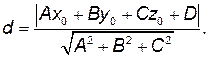
В нашем случае:

Ответ: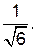

№10. Вычислить пределы:

а) .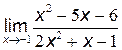

Решение:

При 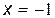числитель и знаменатель дроби обращаются в нуль, то есть мы имеем неопределённость вида 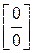. Разложим числитель и знаменатель на множители:

Квадратное уравнение 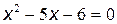имеет корни 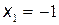, 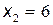. Значит, .

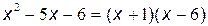Квадратное уравнение 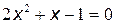имеет корни 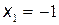, 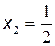. Значит, .

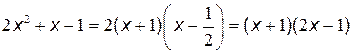Поэтому .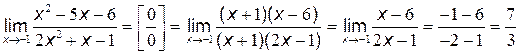

Ответ: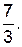

б) .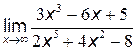

Решение:

При 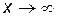числитель и знаменатель дроби также стремятся к бесконечности, то есть мы имеем неопределённость вида .

,

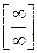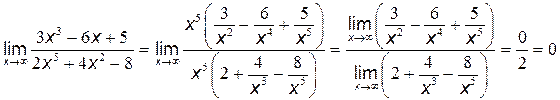так как частные 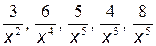стремятся к нулю при .

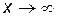Ответ: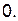

в) .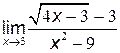

Решение:

При 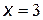числитель и знаменатель дроби обращаются в нуль, то есть мы имеем неопределённость вида 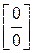. Для раскрытия этой неопределённости умножим числитель и знаменатель дроби на выражение, сопряжённое числителю: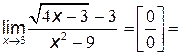

.

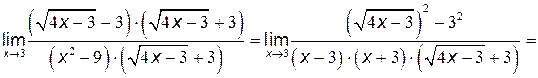
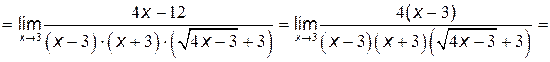
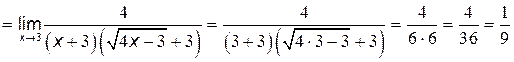Ответ: .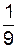

г) .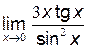

Решение:

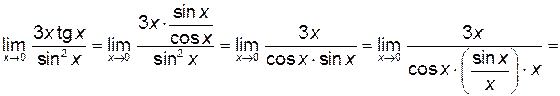
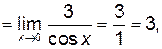так как 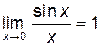(первый замечательный предел), а .

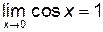Ответ: .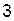

№11. Вычислить 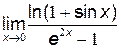, используя эквивалентные бесконечно малые функции.

Решение:

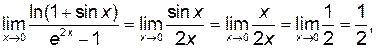так как 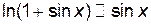, , 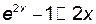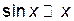при .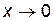

Ответ: .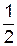

№12. Исследовать функцию 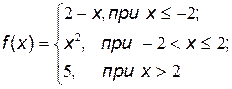на непрерывность и построить её график.

Дата добавления: 2015-08-20