Поле линейной системы идентичных излучателей.

Выражение (3.6) можно упростить в случае расположения излу­чателей вдоль прямой линии на одинаковых расстояниях друг от друга. Такая система излучателей называется линейной системой или линей­ной решеткой.

На рис. 3.1 показана линейная система из n идентичных излу­чателей, расположенных на одинаковых расстояниях друг от друга. Пусть линия расположения излучателей совпадает с полярной осью (z) сферической системы координат, начало которой находится в центре излучателя 1. Тогда направление на точку наблюдения, расположен­ную на достаточно большом удалении, будет определяться меридио­нальным углом сферической системы координат. Из рис. 3.1 следует, что

(3.8)

Подставляя (3.8) в(3.3), получаем

Напомним, что 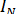и 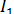- комплексные амплитуды токов.

Абсолютное значение (модуль) выражения (3.9) определяет собой диаграмму направленности линейной системы идентичных излучателей.

Множитель является множителем решетки, определяющим диаграмму направлен­ности линейной системы ненаправленных излучателей. Выражение (3.10) показывает, что эта диаграмма не зависит от азимутального угла 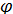сферической системы координат. Это обстоятельство позволяет применять правило перемножения диаграмм направленности для любой плоскости 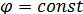в пространстве, используя один и тот же множитель си­стемы (3.10).

Выражение (3.10) можно существенно упростить для случая линейной системы с излучателями, у которых амплитуды то­ков одинаковы, а фазы меняются по ли­нейному закону. Такие системы иногда называются равномерными линейными ре­шетками. Подобные антенные системы не являются характерными для общего слу­чая, однако они часто встречаются и по­тому представляют практический интерес.

Рис. 3.1. Линейная систе­ма идентичных излучателей.

Поскольку при рассмотрении данного вопроса нас будет интересовать лишь отно­сительное изменение напряженности поля в разных направлениях, амплитуды токов I _N всех излучателей можно принять рав­ными единице.

Линейный закон изменения фазы токов можно записать в виде

где - угол сдвига фаз между токами соседних излучателей; то есть предполагается, что

Подставляя (3.12) в (3.9) и учитывая, что амплитуды токов приняты равными единице, получаем

В выражение (3.13) входит сумма n членов геометрической про­грессии, первый член которой равен единице, а знаменатель где .

Сумма n членов геометрической прогрессии

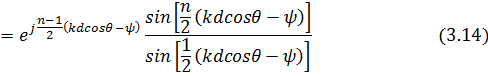
Подставляя (3.14) в (3.13), получаем

Последнее выражение является очень важным в теории антенн.

Остановимся на нем подробнее. Множитель

в показателе есть расстояние от середины антенной системы до точки наблюдения, определяет фазовый угол тока, соответ­ствующего той же средней точке антенны. При указанных обозначе­ниях выражение (3.15) можно переписать так:

Модуль выражения 3.16) определяет собой амплитудную характе­ристику направленности рассматриваемой системы направленных из­лучателей. Фазовый множитель выражения (3.16)

определяет фазовую характеристику системы, а следовательно, форму ее волновой поверхности (поверхности равных фаз). При сферической форме волновой поверхности ее центр называется фазовым центром антенной системы.

Однако некоторые антенны особенно на СВЧ не имеют фазового центра. Для таких антенн поверхности равных фаз отличаются от сферических поверхностей. На рис. 3.2 показаны линии постоянной фазы для рупорной антенны, отличающиеся от дуг окружности (с цент­ром Р), которые для сравнения изображены пунктиром. Амплитуда поля системы излучателей отличается от амплитуды ноля одиноч­ного излучателя множителем:

Это выражение определяет собой диаграмму направленности линейной системы из п ненаправленных излучателей и является так называемым множителем решетки.

Рис. 3.2. Поверхности постоян­ных фаз электромагнитной волны у антенны, не имеющей фазового центра.

Из (3.16) следует, что общее выражение для диаграммы направ­ленности линейной системы из n на­правленных излучателей определяется произведением

Выражение (3.18) определяет ненор­мированную диаграмму направлен­ности системы из n ненаправленных излучателей, так как его максималь­ное значение отличается от единицы и равно n при

Действительно, при этом выражение (3.18) превращается в неопределен­ность вида. Учитывая, что в квад­ратных скобках выражения (3.18) стоят аргументы, стремящиеся к нулю, синусы можно заменить аргументами и тогда в пределе

Нетрудно убедиться, что n определяет максимально возможное зна­чение выражения (3.18). Поэтому нормированное значение этого вы­ражения будет

В том случае, когда направление максимума диаграммы одиночного излучателя совпадает с направлением, для которого получается мак­симум множителя системы, можно написать выражение для нормиро­ванной диаграммы направленности системы направленных излучате­лей в виде

Определим далее выражение для диаграммы направленности не­прерывной линейной системы, составленной как бы из бесконечно близко расположенных ненаправленных излучателей. Для этого мож­но воспользоваться выражением (3.22), полагая, что п (смотри (3.21) - (3.23)), где L - длина системы:

В последнем выражении отношение представляет собой сдвиг фаз на единицу длины системы, и его можно трактовать как волновое число некоторой электромагнитной волны, распространяющейся вдоль линейной системы со скоростью - частота колебаний; длина волны в рассматриваемой системе.

Учитывая это, можно произвести следующие преобразования:

где - длина волны в свободном пространстве; - так называемый коэффициент укорочения волны.

Подставляя (III.25) в (III.24) и меняя местами cos 0 и £ как в чис­лителе, так и в знаменателе, получаем

^(1-cosO).

(III.26)

F_n(0) = sinpy(i-cos0)

Это выражение при 5 > 1 имеет максимальное значение, меньшее чем единица. Оно определяет собой ненормированную диаграмму на­правленности непрерывной линейной системы равноамплитудных ненаправленных источников, вдоль которой фаза меняется по такому же закону, как и в бегущей волне.

В случае непрерывной линейной синфазной системы, для которой ■ф = 0, из (111.24) получаем

)/

kL

(III.27)

cos 0.

KL

F_n (0) = sin ■—- cos 0

Если отсчет углов вести не относительно линии расположения излу­чателей, а относительно направления максимума излучения, которое перпендикулярно этой линии, то угол 0 надо заменить на угол Ф, свя­занный с 0 равенством 0 = 90° — Ф. После такой замены выражение (111.27) принимает вид

^KL

(III.28)

/„(Ф) = мп

Полученные выше выражения (III.18), (111.19), (III.22), (111.23), (111.26) — (III.28) позволяют рассмотреть вопрос о направленном дей­ствии многих типов антенн, применяемых на практике. Используем их для исследования некоторых типов антенных систем.

а) Два излучателя при разных фазовых соотношениях и расстоя­ниях между ними. При п = 2 выражение (III. 18) принимает вид

: 2 cos [(Kd cos 8 — iJj)/2]. (III.29)

sin [(Kdcos 0 —\|))/2]

Это выражение определяет диаграмму направленности двух нена­правленных излучателей, разнесенных на расстояние d, стоками, сдви­нутыми по фазе на угол ф. В частности, это может быть диаграмма на­правленности двух вертикальных вибраторов в горизонтальной плоскости.

(III.30)

Рассмотрим несколько частных случаев. Пусть d = Я/2, tJj = 0, тогда

f_n (8)= 2 cos cos 8

Это выражение обращается в нуль при 6 = 0 и 180° и имеет максимум при 6 = 90°. Результирующая диаграмма направленности изображена на рис. III.3, а; знаки «-)-» означают, что токи вибраторов совпадают по фазе.

Такая антенная система, называемая синфазной (Ф = 0), харак­теризуется тем, что максимумы излучения получаются в направ­лении, перпендикулярном линии расположения излучателей. В этом

Рис. III.3. Горизонтальная диаграмма направленности двух синфазных верти-

sin [(Kd cos 0 — \|))]

ш

X

кальных вибраторов, расположенных на расстоянии d = ^(а); векторные диаграм­мы сложения полей (б).

направлении длина пути от каждого излучателя до точки наблюдения будет одинаковой. Поэтому векторы напряженностей полей, созда­ваемых каждым из вибраторов, будут в фазе, так как поля в указанном направлении будут запаздывать на одно и то же время относительно токов в вибраторах. Минимумы излучения (нули) получаются вдоль линии расположения излучателей. Это объясняется тем, что волны, излучаемые двумя синфазными источниками, в этом направлении проходят пути, отличающиеся между собой на половину длины волны.

В результате волны, попадающие из источников в точку наблюдения, оказываются в противоположных фазах. Соответствующие векторные диаграммы сложения нолей показаны на рис. II 1.3, б. Пусть d = к/2, ij) --- я, тогда

2я к

/„(9) = 2 cos

-^-cose— я]' =2sin^cose). (Ill.31)

Это выражение обращается в нуль при 0 = ± 90° и имеет максимум при 0 = 0 и 180°. Соответствующая диаграмма направленности изо­бражена на рис. II 1.4, знаки «-)-» и «—» означают, что токи вибрато­ров находятся в противофазе.

Рис. [[[.4. Горизонтальная диаграмма на­правленности двух вертикальных вибрато­ров с токами в противоположных фазах.

Рассмотренная антенная система, называемая иногда переменно- фазной = 180°), характеризуется тем, что максимумы излучения получаются вдоль линии расположения излучателей, а минимумы (ну­ли) — в направлении, перпендикулярном этой линии. Такая форма диаграммы направленности обусловлена интерференцией полей двух источников, подобной рассмотренной выше для синфазных излу­чателей.

Рис. 111.5. Горизонтальная ди­аграмма направленности верти­кальной антенны с рефлектором.

Пусть d = к/4, \|) = я/2, тогда

9-—11 2 /'.

[f«-

2л к

(111.32)

= 2 cos

-cos 0)

fn (9) — ^ c°s

cos

Зто выражение обращается в нуль при 0 = 180° и имеет максимум при 0 = 0°. Общая диаграмма направленности изображена на рис. II 1.5. Как видно из рисунка, диаграмма напоминает собой кар­диоиду. Такая диаграмма является характерной для так называемой антенны с рефлектором** Лзеркалом). Волны, излучаемые антенной, как бы отражаются от рефлектора, расположенного позади антенны на расстоянии в четверть длины волны. Для того чтобы получилась указанная на рисунке шрдиоидная диаграмма, амплитуды токов

*> Слово рефлектор происходит от английского глагола reflect — отражать.

73

антенны и рефлектора должны быть одинаковыми, а ток в рефлекторе должен опережать по фазе ток в антенне на 90

Подобную же диаграмму направленности будет иметь антенна с так называемым директором*). Директор представляет собой виб­ратор, расположенный впереди антенны на расстоянии в четверть длины волны, проходящий по нему ток должен иметь такую же ам­плитуду, как и токе антенне, и отставать от него по фазе на 90°. При этом условии излучение будет получаться максимальным в сторону директора и минимальным в обратном направлении (рис. III.5).

Необходимый сдвиг фаз между токами в вибраторах получается с помощью соответствующей схемы питания или настройки.» Рефлек-

	\ /	^v"
1 +	+ 1 V +/

Рис. 1X1.6. Диаграмма направленности двух ненаправленных близко располо­женных излучателей: о — при синфазных токах; б — при токах в противофазе.

тор, питаемый от генератора при помощи фидера, называется актив­ным. Рефлектор может быть также пассивным, когда он не питается от фидера, а возбуждается полем питаемой антенны. В этом случае под­бор фазы тока в рефлекторе достигается соответствующей настройкой.

Директоры, как правило, выполняются пассивными.

В заключение рассмотрим случай двух близко расположенных, ненаправленных вибраторов (когда d X).

Пусть 1|з = 0. Тогда из (II 1.29) имеем

/_n(0) = 2cos ^Ыс₂^[1] = 2cos^cos8)~2, (Ш.ЗЗ)

так как (nd/X) cos 8 независимо от 8 — величина малая. Соответствую­щая ненаправленная диаграмма в полярных координатах изображена на рис. III.6,а.

(III.34) • направ­

Пусть 1|з = 180°. Тогда из (III.29) получаем

f_n (6) ■= 2 cos (Kd cos 0 — я) = 2 sin (-у- к d cos 6 j ~ Kd cos 0,

так как при малых аргументах синус можно заменить самим аргу­ментом. Множитель Kd на форму диаграммы направленности не влияет, она определяется лишь множителем cos 9 (рис. III. 6, б). При одина­ковых токах в излучателях поле и соответственно действующая высота у синфазной системы будут много больше, чем у противофазной.

б) Синфазная система ненаправленных излучателей. Исследуем основные свойства диаграммы направленности линейной системы, составленной из п ненаправленных синфазных излучателей. Используя выражение (III 18) при = 0, получаем

Г п (п \

sin —(/cacosO—iji) sin —кй cos 0

sin j — (Kd cos 0 —г|>)

fn (9) = ■——-------------------- ^V----------- '

(III.35)

sin | Kd cos 0)

^ /

Определим углы 9, при которых значения диаграммы обращаются в нуль. Выражение (III.35) обращается в нуль, когда числитель

sin /cdcos =0, (III.36)

при условии, что знаменатель (III.35) в нуль не обращается. Из (III.36 следует, что кй cos 9 = тл, где т = 0; ± 1; ± 2;...; откуда

cos 9 =------------------------- =----. (III.37)

(/г/2) (2лД) d nd '

Нетрудно заметить, что при т = 0 9 = 90° и знаменатель (II 1.35), так же как и числитель, обращается в нуль, что дает для выражения (II 1.35) неопределенность вида 0/0. Эта неопределенность легко рас­крывается [см. (III.21)], после чего получается

fn (⁰)|₀=9О° =^п- (II 1.38)

Значение п определяет собой максимум диаграммы направленности, который ориентирован в направлении, перпендикулярном линии рас­положения излучателей. Это значение в п раз больше, чем напряжен­ность поля, создаваемого одиночным излучателем в любом направле­нии, что следует из (III.35) при п = 1. В направлении максимума диа­граммы все напряженности полей отдельных излучателей склады­ваются в одинаковой фазе, т. е. арифметически.

Подобные же максимумы получаются и в направлениях, опреде­ляемых из условия равенства нулю знаменателя выражения (III.35),

когда -i- кй cos 0 = ± л; ± 2 л;... и далее, т. е. в направлениях,

для которых

_COs9=± — — =; cos9=± —,... (111.39)

2л d d d '

Однако, если ограничиться небольшими расстояниями между излуча­телями й < Я, равенства (111.39) не могут выполняться, и тогда для рассматриваемой системы излучателей получается лишь один так

75

называемый главный максимум (или лепесток) в направлении, пер­пендикулярном линии расположения излучателей (0 = 90").

Направления нулевого излучения определяются из выражения (111.37)"

cosQ = mX/nd,

где m = ± 1; ± 2;... и \mX/nd\ = |cos 0| ^ 1.

Эти выражения показывают, что чем больше протяженность си­стемы излучателей (nd) по сравнению с длиной волны, тем больше на­правлений нулевого излучения и тем больше лепестков диаграммы направлен­ности, расположенных между указан­ными направлениями.

На рис. III.7 для примера изобра­жена диаграмма направленности син­фазной системы из шести ненаправлен­ных излучателей, разнесенных на пол­волны друг от друга (диаграмма в плоскости их расположения). Простран­ственная диаграмма направленности получается в виде поверхности как ре­зультат вращения фигуры рис. III.7 вокруг линии расположения излучате­лей. Если увеличить число излучате­лей, сохранив неизменным расстояние между ними, получится более узкий главный лепесток диаграммы направлен­ности и большее число боковых лепе­стков.

Ширину диаграммы направленности (главного лепестка) линейной синфазной системы ненаправленных излучателей, если ее определить как угол 2 0_О между направлениями нулевого излучения (ближайшими к углу 0 = 90°), можно определить с помощью выражения (III.37), пола­гая т = 1,

Рис. III.7. Диаграмма направ­ленности синфазной системы из шести ненаправленных излуча­телей, разнесенных на пол­волны.

sine о = X/nd. (II 1.40)

(III.41)

(II 1.42)

Для остронаправленных антенн, т. е. при больших nd, sin 0_О можно заменить углом 0_О и тогда

2 0 о ~ 2 X/nd.

Переходя от радиан к градусам и обозначая длину антенны (п — 1)d ~ nd = L, получаем

(2 0 ₀)° ^ 115 X/L.

Определим далее угол 20_{о 5} — ширину диаграммы направлен­ности рассматриваемой системы излучателей по половинной мощно­сти как угол между направлениями, вдоль которых поле уменьшается
в 1^2 раз по сравнению с полем в направлении максимума (рис. Ш.8). Пронормируем выражение (II 1.35):

F_n(9)=-i-/_n(9) = sin ^JL KdcosB)j n sin J-j-_Kdcosej. (111.43)

В направлении 9 = 90° F_n (9) = 1. В направлении 9 = л/2 — 9_0iS = ^sin [-j- к-d sin n sin (0,5Kd sin 6_0j5). (III.44)

Для определения ширины 29_{0 5} диаграммы направленности необ­ходимо решить уравнение (III.44) относительно 0_{О 5}. Это уравнение трансцендентное и может быть решено одним из приближенных ме­тодов, например графическим путем.

В некоторых случаях уравнение (III.44) может быть упрощено и решение для 9_{0 б} получено в легко запоминающемся виде. Это от­носится к остронаправленным антенным системам, для которых sin (0,5 кй sin 9) в пределах главного лепестка (где углы 9 малы) можно заменить аргументом 0,5«:cfein9.

При этом выражение (III.44) принимает вид

F_n (9_{0 5}) ~ sin ^y Kd sin 9_0i6 j j-j- Kd sin 9_0>6 = sin x/x = 0,707, (111.45) где

x~~ Kd sin 9_{0 5}. (III.46)

Функция sin x/x в зависимости от x показана на рис. III.9. Эта кривая представляет собой в декартовых координатах обобщенную диаграмму направленности линейной системы синфазных излучателей

77

с токами равной амплитуды. Как видно из графика, значение sin*/* — 0,707 получается при л; = 1,394 рад, т. е.

х — — Kd sin 9„, =■- 1,394,

2 ".о

следовательно,

1,394.2 nd2n/X

sin 0,

0,444 — nd

'0,5

Для остронаправленных антенных систем, имеющих значительную протяженность L = (п — I) d ~ nd, когда sin 0_Oi5 с* G_{0 5}, получаем

0_О,₅ = 0.444A./L.

Ширина диаграммы

(III.4 7)

(20_о,₅)°

(III.48)

29₀,5 ~ 0,888?i/L (рад)

или

С, ⁵' /

Это простое выражение показывает, что ширина диаграммы направленности рас­смотренной антенной системы обратно пропорциональна длине антенны (L), вы­раженной в долях волны (Я). Из рис. II 1.9 видно, что первый боковой лепесток диа­граммы направленности по полю имеет максимальное значение, равное 21% от максимума основного лепестка (что соответствует 4,4% от максимума диаграммы по мощности), вто­рой боковой лепесток 13% (или 1,8% от максимума диаграммы по мощности) и т. д.

Sxnx х Ю

\
\
\	0,21		0,13
ж		/	Ьг зж

0,5

Рис. II 1.9. Обобщенная ди­аграмма направленности ли­нейной синфазной равноампли- тудной системы.

Диаграммы направленности непрерывной линейной системы с током неизменной амплитуды и фазы по длине похожи на соответствующие диаграммы направленности системы из дискретных источников. Для непрерывной системы, составленной из ненаправленных источников, на основании (II 1.28) можем записать

kL

F_n(0) = sin(-^sin0

Если обозначить

(111.49)

kL

₂ sin 9 = у, тогда

sin Q.

F_n (9) = sin у/у.

Последнее выражение совпадает с выражением (II 1.45) и имеет вид кривой, изображенной на рис. III.9. Из рисунка видно, что диаграмма направленности непрерывной сннфазной системы имеет максимум при у = 0, когда 0 = 0, т. е. в направлении, перпендикулярном ли­нейной системе.

Первый нуль диаграммы направленности получается в направле­нии 0_о, определяемом из условия

-- - in 0_U =,- л; sin 0_О =—

Следовательно, для остронаправленных антенн ширина диаграммы по нулевым значениям будет определяться полученными ранее выра­жениями (III.41), (III.42).

Выражение для ширины диаграммы по половинной мощности будет также совпадать с полученным выше выражением (111.48).

в) Система ненаправленных излучателей при наличии сдвига фаз между их токами. Исследуем основные свойства диаграмм направлен­ности линейной системы из п ненаправленных излучателей с токами, сдвинутыми по фазе на одинаковый угол я]з. Сначала рассмотрим си­стему из дискретных источников, а затем непрерывную систему.

Нормированная диаграмма направленности системы дискретных источников

F_n(B) = sin

(III.22)

-^-(/cdcosQ — n sin j^-i- (/cdcos9—i|>)

Это выражение имеет максимум (равный единице) при выполнении условия (III.20):

KdcosQ_m — = 0,

откуда

cos0_m = ^!кй = я|Л/2 nd, (111.50)

причем |cos9_m| =|т|Л/2я^|< 1.

Выражение (111.50) показывает, что направление максимума из­лучения (9_т) зависит от угла г|) — сдвига фаз между токами соседних излучателей и может меняться в широких пределах. При я]з = 0 — случай рассмотренной выше синфазной системы 9_m = ± 90° мак­симум получается в направлении, перпендикулярном линии располо­жения излучателей. При if = 2 яd/'X; cos Q_m = 1 и Q_m = 0 максимум получается вдоль линии расположения излучателей в том направле­нии, в котором происходит убывание фазы токов излучателей.

В противоположном направлении, т. е. для 0 = 180°,

F_n (0) = sin (md)/nsinKd. (111.51)

Отметим, что сдвиг фаз г|) = 2 яd/X равен запаздыванию по фазе бегу­щей волны при распространении от, одного излучателя до соседнего.

Для примера на рис. III.10 показаны диаграммы направленности в плоскости линейной системы из ненаправленных излучателей при разных сдвигах фаз яр. Из рисунка видно, что поворачивается макси­мум излучения по мере изменения сдвига фаз i|>; это изменение направ­ления называется качанием луча и используется для обзора прост­ранства в некоторых радиолокационных и радионавигационных системах.

Далее рассмотрим непрерывную линейную систему ненаправлен­ных источников. Направленные свойства такой системы похожи на свойства рассмотренной системы дискретных источников. Нормирован­ная диаграмма направленности такой системы определяется выра­жением (III.26), имеющим максимум (равный единице) при

= е,

cos 0„

(III.52)

где £ определяется (III.25). Условие (II 1.52) может выполняться для

значений £* лежащих ь пределах

0<£<1. (III.53)

Случай £ = О, соответствующий синфазной системе, рассматри­вался выше; при этом максимум излучения получается в направлении, перпендикулярном линии расположения излучателей.

5=0°

Рис. ШЛО. Диаграммы направ­ленности линейной системы из не­направленных дискретных излуча­телей при разных сдвигах фаз.

При 1=1 cos0_MaKC = 1 и 0_макс = О, Т. е. максимум получается вдоль линии излучателей и направлен в сторону убывания фазы токов системы; это соответствует направлению движения бегущей волны, как бы возбуждающей систему рассматриваемых источников.

При значениях 0 < £ < 1 направление максимума излучения образует острый угол относительно линии излучателей.

Практически возможен случай £ > 1, когда условие (II 1.52) полу­чения максимума, равного 1, не может быть выполнено, так как ни при каких значениях 0 cos0 не может быть больше 1 и F_n (0) получает­ся меньшим 1. Характер диаграммы направленности изменяется в за- 80

висимости от того, насколько £ отличается от 1. При значениях близ­ких к 1, максимум диаграммы (хотя и меньший, чем 1) сохраняется в направлении 0 = 0, т. е. вдоль оси системы. При дальнейшем уве­личении £ значение функции, определяющей диаграмму для направ­ления вдоль оси системы, постепенно уменьшается и при некотором значении £ (£ = 1 -f- K/L) может даже обратиться в нуль.

На рис. III.11 показаны примеры диаграмм направленности линей­ной непрерывной системы излучателей при разных значениях £.

г) Система направленных излучателей. Рассмотрим некоторые примеры систем, для определения направленного действия которых используется теорема перемножения диаграмм.

Полуволновый вибратор с рефлектором. Определим диаграмму на­правленности системы из двух вибраторов длиной полволны каждый, расположенных параллельно и разнесенных на расстояние в четверть волны (рис. 111.12). Ток рефлектора опережает по фазе ток антенны' на угол 90°.

Диаграмма направленности в плоскости, проходящей через виб­раторы, имеет вид

F (ф, 0) = F, (ф, 0) F_n (9). (111.23)

Здесь Fj (ф, 9) — диаграмма направленности отдельно взятого полу- волнового вибратора, которая при указанном на рис. III. 12, а отсчете углов 9 определяется уравнением

(ф, 9) = cos sin 0 j /cos 9

F_n (9) = cos

и имеет вид, показанный на рис. III. 12, б; F_n (9) — множитель си­стемы, представляющий собой диаграмму направленности двух нена­правленных излучателей, разнесенных на расстояние в четверть волны с токами, сдвинутыми по фазе на 90°. Для подобной системы излуча­телей выше было получено выражение (III.32), которое после нормиро­вания имеет вид

^-(1 —cos9)j. (III.54)

Соответствующая этому выражению диаграмма приведена на рис. III.12, в.

Диаграммы направленности F _х (ф, 9) и F_n (9) имеют максимумы в одном направлении.

Результирующая диаграмма направленности в плоскости антенны с рефлектором определяется произведением

cos (— sin 9

F (_ф, 9) = —^ cos

(III.55)

-j(l—cos0)

' cos 0

и имеет вид, показанный на рис. III. 12, г. Эта кривая может быть по­строена в результате вычислений с помощью выражения (111.55) или графически путем перемножения кривых рис. 111.12, б и 111.12, в.

so"

Рис. 111.12. Полуволновый вибратор с рефлектором (а); его диаграмма направ­ленности (б); диаграмма множителя системы (в); диаграмма направленности в плоскости вибратора и рефлектора (г).

Выражение (III.55) справедливо для плоскости, в которой распо­ложены вибраторы, т. е. для плоскости хОг (рис. III. 12, а). Это выра­жение нетрудно обобщить на случай пространственной диаграммы на­правленности, т. е. для определения относительной величины напря­женности поля в любой точке пространства со сферическими коорди­натами <р и 9.

Будем считать, что линия, вдоль которой расположены вибраторы,

Гя

совпадает с осью г. Тогда множитель системы cos — (1 — cos 8)] ос­тается неизменным. С другой стороны, выражение для диаграммы на­правленности одиночного вибратора изменится и будет иметь вид а

.., Н К ^2

/=\((p,9) = cos cosaj/sina, ' ^{1 1 1,л} ' ' ' ¹ р—|

(III.56)

где a — угол между осью вибратора ^Рис- ^1ПЛЗ- Провод длиной L с бе-, _ч _ гущей волной тока.

(осью х) и направлением на точку ^у

наблюдения.

Между углами а, 0 и ф существует следующая связь: cos a = sin 0 cos ф; sina = УI — sin² 0 cos² ф,

поэтому

Ft (ф, 9) = cos — sin 0 cos (p J/Kl — sin²9 cos² ф, (III.57)

и выражение для пространственной диаграммы направленности полу- волнового вибратора с рефлектором примет следующий вид:

cos I — sin 0 cos <р ]

F(ff,Q) = — ^{K 2} L cosf — (1 —cos6)1. (III.58)

™ ' /I -sin³ 0 cos² ф L 4 ^V J

Это выражение превращается в (III.55) в случае ф = 0° (т. е. в пло­скости хОг). ■

Провод с бегущей волной тока. Рассмотрим провод длиной L (рис. III. 13) с бегущей волной тока. При ориентации провода вдоль оси г уравнение для тока имеет вид

/₂ = /₀ехр(— }кг), (III.59)

где/₀ — ток в начале провода; к = 2л/X = со/о; v — скорость рас­пространения волны вдоль провода; X — длина волны в проводе.

Разделим мысленно провод на большое число п одинаковых эле­ментов. Длина каждого элемента d = Lin, расстояние между их центрами также равно d. Соседние элементы возбуждаются с разно­стью 4аз = 2лd/X = Kd.

Диаграмму направленности всего провода можно определить как диаграмму системы из п направленных излучателей, т. е. как произ­ведение

F (ф, 6) = A₁F₁ (ф, 6) F_n (0),

где 0 — угол, отсчитываемый относительно линии расположения эле­ментов; Fj (ф, 0) — диаграмма одиночного элемента провода; F_n (0) — диаграмма линейной системы из п ненаправленных излучателей, раз­несенных на расстояние d друг от друга, с токами, сдвинутыми по фазе на угол ij; = Kd; А_х — нормирующий множитель, его введение необ­ходимо потому, что направления максимумов (равных единице) для множителей F_у и F_n в общем случае не совпадают.

Рис. III.14. Диаграммы направленно- Рис. 1П.15. Диаграмма направленно­сти провода с бегущей волной при ности провода с бегущей волной при L=0,5Я. L=5Я.

При достаточно большом п длину каждого элемента можно считать малой по сравнению с длиной волны и тогда, как и для элементарного диполя, F-t (ф, 0) = sin 0. Множитель системы F_n (6) определяется формулой (111.26).

Следовательно, общее выражение для нормированной диаграммы направленности провода с бегущей волной

Г 1

sin — — cos 9)

/=-(ф,0) = А51П0-У------------------ (III.60)

— (5-cos 9)

Сомножитель sin 0 = 0 при 0 = 0, сомножитель F_n (0) при 0 = 0 обычно имеет максимальное значение. Поэтому результирующая диаг­рамма направленности в плоскости провода имеет максимум под не­которым острым углом к оси провода.

На рис. III. 14 и III. 15 приведены примеры диаграмм направлен­ности провода с бегущей волной для проводов разной длины и не­скольких значений Пространственные диаграммы направленности получаются в результате вращения фигур, изображенных на рисунке, вокруг провода как вокруг оси.

Как видно из рисунка, провод с бегущей волной обладает диаграм­мой направленности, максимальные значения которой располагаются
в пределах одной полусферы. Для провода значительной длины глав­ные лучи диаграммы как бы образуют воронку, которая сужается по мере увеличения длины провода; углы раствора основных лепестков при этом уменьшаются, К таким же результатам приводит и увели­чение коэффициента £ (т. е. уменьшение скорости распространения волн в проводе).

*> Слово директор происходит от английского глагола direct

лять. 74

Дата добавления: 2015-08-17