Задача про розподіл капіталовкладень між підприємствами.

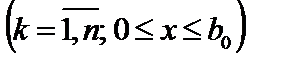Планується на наступний рік діяльність виробничої системи, яка складається з n підприємств. Відома початкова сума коштів — , що має бути розподілена між всіма підприємствами. Сума вкладень х приносить k -му підприємству прибу­ток . Значення функції , задані таб­лицею.

Необхідно визначити — кошти, які потрібно виділити k -му підприємству так, щоб отримати максимальний сумарний прибуток від вкладення коштів в усі підприємства .

Позначимо кількість коштів, що залишилися після k -го кроку (тобто кошти, які необхідно розподілити між рештою (n – k) підприємств через :

.

Задача розв’язується поетапно. В даному разі етапами є вкладення коштів в кожне підприємство.

І етап. Кошти вкладаються лише в одне (наприклад, перше) підприємство. Найбільший прибуток (ефективність першого етапу), що може бути отриманий, позначимо через 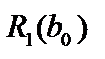. Маємо:

.

ІІ етап. Порівняємо ефективність, яку отримаємо, вкладаючи кошти лише у перше підприємство та вкладаючи кошти одночасно і в перше, і в друге підприємства. Якщо позначити ефективність другого етапу через , то отримаємо:

.

Для k -го етапу маємо рекурентне співвідношення:

.

Послідовно розв’язуючи отримані рівняння, визначаємо оптимальні рішення на кожному етапі.

1.8.Динамічне програмування та галузь його застосування

Всі економічні процеси та явища є динамічними, оскільки вони функціонують і розвиваються не тільки у просторі й у часі. Для народного господарства в цілому, його галузей, регіонів чи окремих підприємств з метою їх стабільного функціонування та розвитку необхідно розробляти стратегічні та тактичні плани. Стратегічні плани містять параметри діяльності об’єктів, які характеризують їх віддалене майбутнє. Отже, вони мають розроблятися на основі динамічних моделей, для знаходження розв’язків яких застосовуються методи динамічного програмування.

Динамічне програмування - метод оптимізації, пристосований до операцій, в яких процес прийняття рішень може бути розділений на окремі етапи (кроки). В основі методу лежить принцип оптимальності, сформульований Р.Беллманом. Оптимальне управління характеризується такими властивостями, що незалежно від початкового стану на будь-якому кроці управління і наступне управління повинно обиратися оптимальним відносно стану, до якого прийде система в кінці цього кроку [3].

Метод, побудований на використанні принципу оптимальності, дозволяє встановити співвідношення між екстремальними значеннями цільової функції в задачах, що характеризуються різною тривалістю процесу і різними початковими станами. При цьому необхідно враховувати наслідки реалізації знайденого оптимального рішення і для наступних рішень. Такий підхід обумовлений розробкою оптимальної стратегії. Процес прийняття рішення в цьому випадку є багатокроковим [2].

При цьому, якщо в задачах лінійного програмування залежності між критеріальною функцією та змінними обов'язково лінійні, то в завданнях динамічного програмування ці залежності можуть мати й нелінійний характер.

Динамічне програмування застосовується в основному для вирішення задач двох класів: планування діяльності економічної системи (підприємств) з урахуванням зміни продукції, що виготовляється в часі відповідно до зміни потреби; перерозподілу ресурсів за різними напрямками в часі.

Найбільш доцільно динамічне програмування застосувати для вирішення таких практичних задач, в яких пошук оптимального рішення вимагає поетапного підходу; наприклад, визначення часу заміни устаткування з урахуванням витрат на експлуатацію устаткування, на придбання нового, первісної вартості даного устаткування, вартості отриманої на ньому продукції [3].

Процес розробки алгоритмів динамічного програмування можна розбити на 4 нижченаведені етапи:

1. Опис структури оптимального розв’язку.

2. Рекурсивне визначення значення, що відповідає оптимальному розв’язку.

3. Обчислення значення, що відповідає оптимальному рішенню за допомогою методу висхідного аналізу.

4. Отримання оптимального розв’язку на основі інформації, отриманої на попередніх кроках.

Етапи 1-3 складають основу методу динамічного програмування. Етап 4 можна пропустити, якщо треба дізнатись тільки значення, що відповідає оптимальному[1].

Існують певні умови,яким має відповідати задача оптимізації, щоб її можна було описати моделлю динамічного програмування. Ці умови такі:

1. Задача може інтерпретуватись як n- кроковий процес управління, а показник ефективності процесу може бути представлений в адитивній формі, тобто як сума показників ефективності на кожному кроці.

2. Структура задачі інваріантна відносно числа кроків п, тобто повинна бути визначена для будь-якого п і не залежати від цього числа.

3. На кожному кроці стан системи визначається кінцевим числом б параметрів стану та управляється кінцевим числом г змінних управління, причому г і в не залежать від кількості кроків п.

4. Вибір управління на К-му кроці не впливає на попередні кроки, а стан на початку цього кроку є функцією лише попереднього стану і обраного на ньому управління (умова відсутності післядії) [3].

Отже, динамічне програмування не є окремим методом розв’язування задач, а являє собою теорію, що поєднує ряд однотипних ідей та прийомів, які застосовуються для розв’язування досить різних за змістом задач.

До задач динамічного програмування належать такі, що пов’язані з оптимальним розподілом капіталовкладень, розподілом продукції між різними регіонами, визначенням найкоротшого шляху завезення товарів споживачам, задачі щодо заміни устаткування, оптимального управління запасами тощо. Динамічне програмування дає змогу прийняти ряд послідовних рішень, що забезпечує оптимальність розвитку процесу в цілому.

Дата добавления: 2015-08-17