Алгоритм методу динамічного програмування

Для розв’язку задачі методом динамічного програмування необхідно здійснити наступні кроки:

1. Вибрати параметри, що характеризують стан керованої системи s на кожному кроці.

2. Розбити операцію на кроки (етапи).

3. Визначити набір крокових управлінь 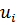для кожного кроку і накладені на них обмеження.

4. Визначити який виграш приносить на i кроці управління 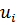, якщо перед цим система була в стані s, тобто записати функцію виграшу:

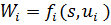
5. Визначити новий стан системи s, в який вона переходить під впливом управління 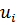на i кроці:

6. Записати основне рекурентне співвідношення динамічного програмування, що виражає умовний оптимальний виграш 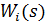через вже відому функцію :

7. Здійснити умовну оптимізацію останнього кроку n, шляхом задання множини станів системи s, з яких можна за один крок дійти до кінцевого стану, обчисливши для кожного з них умовний оптимальний виграш і знайшовши умовне оптимальне управління (s), для якого цей максимум досягається.

8. Здійснити умовну оптимізацію (n - 1) кроку за формулою (1.3.3), при i = (n - 1), (n - 2),... і для кожного з цих кроків вказати умовне оптимальне управління , при якому досягається максимум. На першому кроці змінювати стан системи не потрібно:

9. Провести безумовну оптимізацію управління, використовуючи відповідну інформацію на кожному кроці: врахувавши знайдене оптимальне управління на першому кроці змінити стан системи; для нового стану знайти оптимальне управління на другому кроці і т.д. для кожного кроку. [6], [15]

Дата добавления: 2015-08-17