Решение. На первом шаге, в соответствие с достаточным условием экстремума функции двух

На первом шаге, в соответствие с достаточным условием экстремума функции двух переменных, найдем точки, удовлетворяющие условию:

Частные производные первого порядка от функции равны:

Приравняем их к нулю и решим систему уравнений:

Выпишем отдельно первое уравнение системы и найдем его корни:

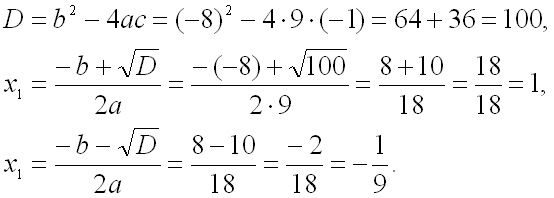
Подставим найденные значения переменной во второе уравнение системы:

и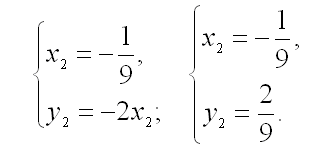

Таким образом, получили две точки 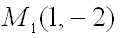и , в которых будет продолжено исследование функции 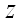на экстремум.

На втором шаге найдем все вторые частные производные от функции :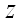

На третьем шаге для каждой из точек 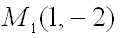и установим наличие экстремума функции 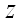(для этого вычислим значения вторых производных и найдем знак дискриминанта в указанных точках).

1) Для точки :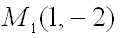

Так как дискриминант больше нуля и 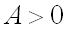, то функция 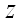имеет минимум в точке :
.

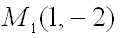2) Для точки :

Так как дискриминант меньше нуля, то функция 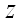не имеет в точке ни минимума, ни максимума.

Ответ: в точке 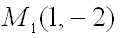функция имеет минимум .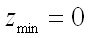

Дата добавления: 2015-08-17