
Читайте также:
|
Проверить, является ли данная стационарная точка функции F (x, y) двух переменных седловой, можно, вычислив матрицу Гессе функции в этой точке: если гессиан будет неопределенной квадратичной формой, то данная точка - седловая. Например, составив матрицу Гессе функции z = x 2 − y 2 в стационарной точке (0,0) получим матрицу:

которая является неопределенной. Поэтому, точка (0,0) данной функции - седловая. Однако вышеприведенный критерий предоставляет только достаточное условие наличия седловой точки. Например, (0,0) является седловой точкой функции z = x 4 − y 4, но матрица Гессе в данном случае будет нулевой матрицей, которую, по определению, нельзя назвать неопределенной.
В общем случае, седловой точкой гладкой функции (чей график изображает кривую, поверхность или гиперповерхность) называется такая стационарная точка, в окрестности которой данная кривая/поверхность/гиперповерхность не лежит полностью на одной стороне касательного пространства в данной точке.
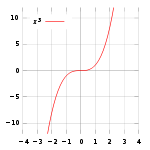

График y = x 3 с седловой точкой в 0
В случае функции одной переменной, седловая точка - такая точка, которая одновременно и стационарная точка, и точка перегиба (точка перегиба не является локальным экстремумом).
Дата добавления: 2015-08-17; просмотров: 74 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение. | | | Необходимое условие экстремума |