Читайте также:
|
Говорят, что функция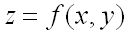 
имеет максимум в точке 
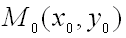, т.е. при 
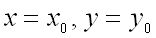, если 
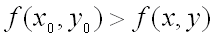для всех точек 
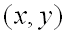, достаточно близких к точке 
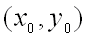и отличных от неё.
Говорят, что функция 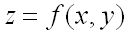имеет минимум в точке 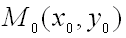, т.е. при 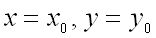, если 
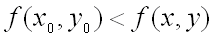для всех точек 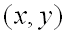, достаточно близких к точке 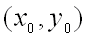и отличных от неё.
Максимум и минимум функции называются экстремумами функции.
Теорема (необходимое условие экстремума функции двух переменных). Если функция 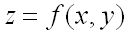достигает экстремума при 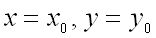, то каждая частная производная первого порядка от 
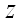или обращается в нуль при этих значениях аргументов, или не существует.
Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку 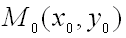функция 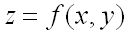имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка 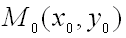является критической точкой функции 
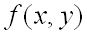, т.е.
,
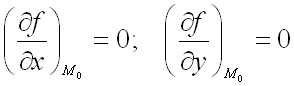тогда при :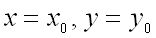
1) 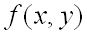имеет максимум, если дискриминант 
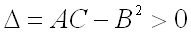и 
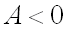, где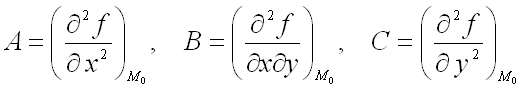 
;
2) 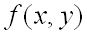имеет минимум, если дискриминант 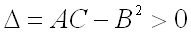и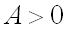 
;
3) 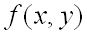не имеет ни минимума, ни максимума, если дискриминант 
;
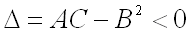4) если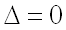 
, то экстремум может быть, а может и не быть (требуется дополнительное исследование).
Дата добавления: 2015-08-17; просмотров: 35 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Сводка и группировка статистических данных | | | Решение. |